深入理解高阶色散
本文存在多个 .GIF 图片,可能会导致网页加载速度慢。
当考虑高阶色散对脉冲传输的影响时,一般为了简便而将脉冲传输方程中的衰减 $\alpha$ 和非线性参数 $\gamma$ 视为 0。同时将脉冲强度 $A$ 归一化处理成 $U$ 。
归一化的脉冲在时域上满足:
$$
\mathrm{i}\frac{\partial U}{\partial z}=\frac{\beta_2}{2}\frac{\partial^2U}{\partial T^2}+\mathrm{i}\frac{\beta_3}{6}\frac{\partial^3U}{\partial T^3}+…
$$
转换到频域变成:
$$
\frac{\partial U}{\partial z}=\mathrm{i}[\frac{\beta_2}{2}(\omega-\omega_0)^2+\frac{\beta_3}{6}(\omega-\omega_0)^3+…]\widetilde U
$$
显示了光脉冲在通过光纤传输时,其包络内的每一个频谱分量都得到一个与频率有关的相移。
频域下方程的通解为:
$$
\widetilde{U}(z, \omega)=\widetilde{U}(0, \omega)\mathrm{e}^{\mathrm{i}\frac{\beta_2}{2}(\omega-\omega_0)^2z+\mathrm{i}\frac{\beta_3}{6}(\omega-\omega_0)^3z+…}
$$
接下来以高斯脉冲为例,单独分析各阶色散对脉冲传输的影响。
在我的GitHub仓库查看源代码。
高斯脉冲的群速度色散
以 $\beta_2>0$ 为例,脉冲中每个频率成分的相移是其与中心频率差的平方。
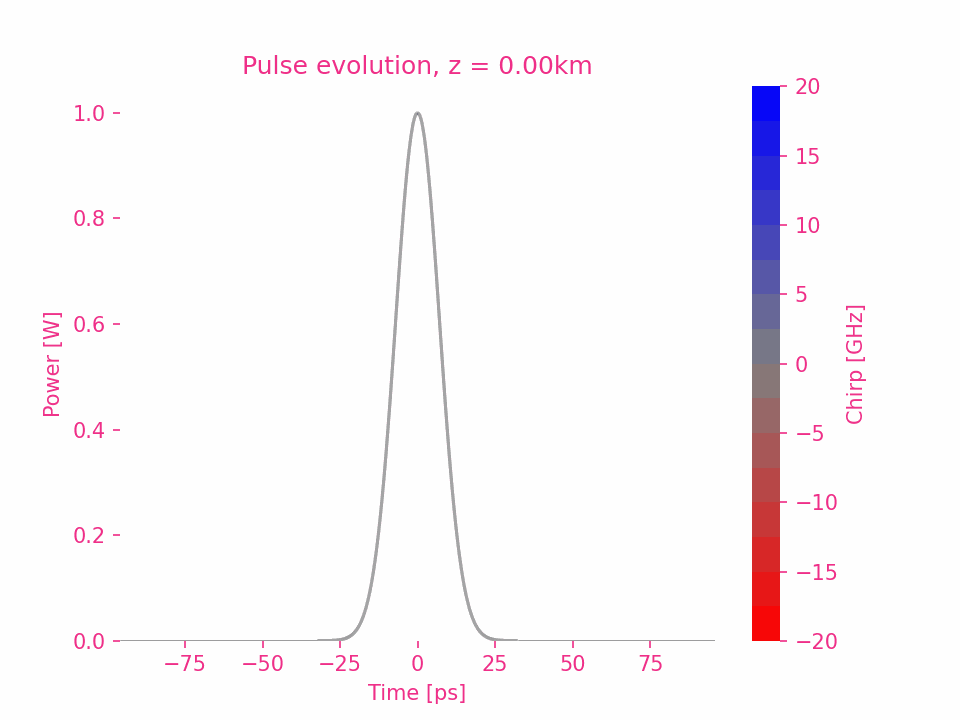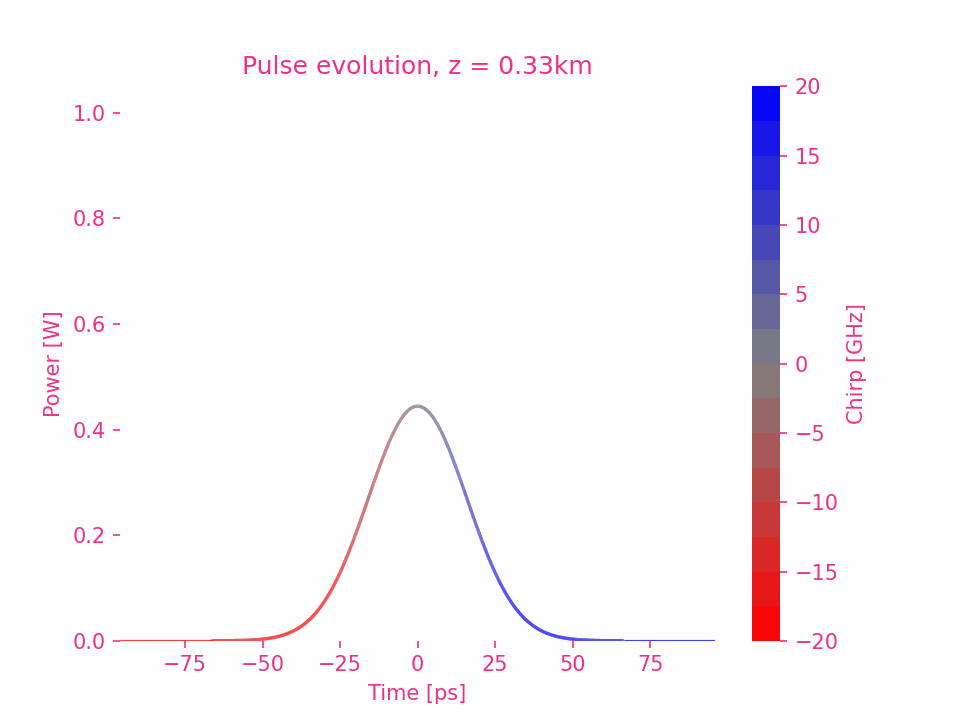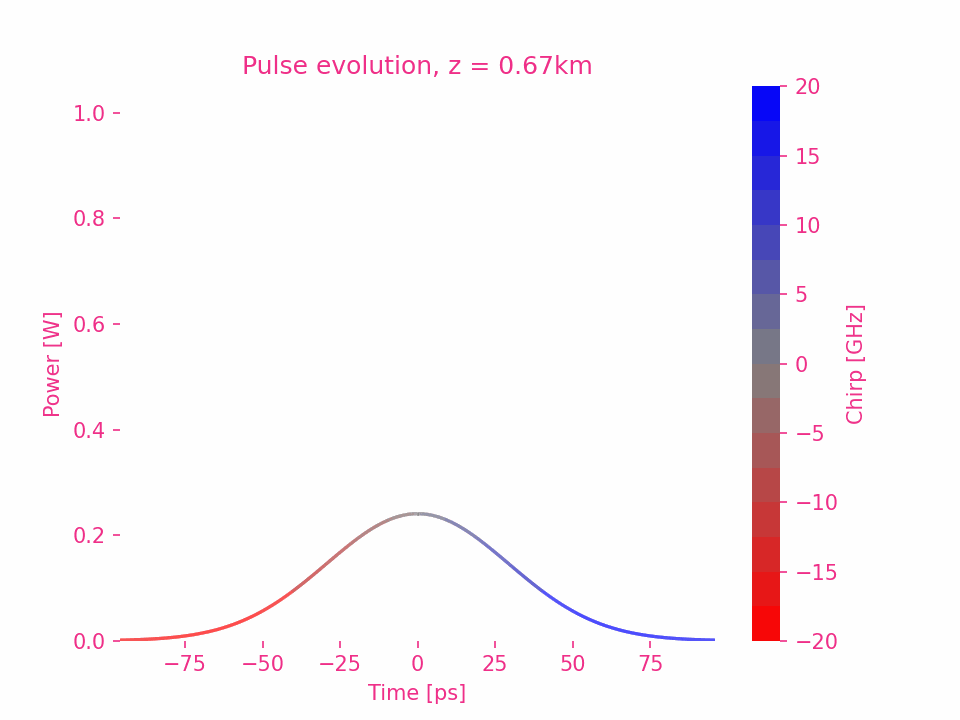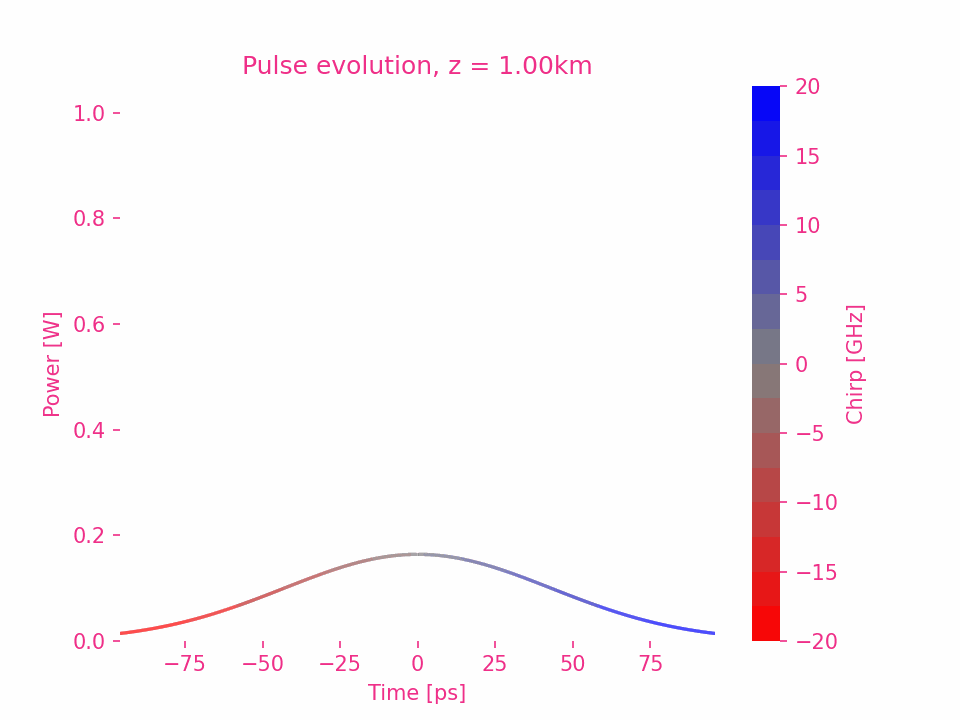
高斯脉冲的三阶色散
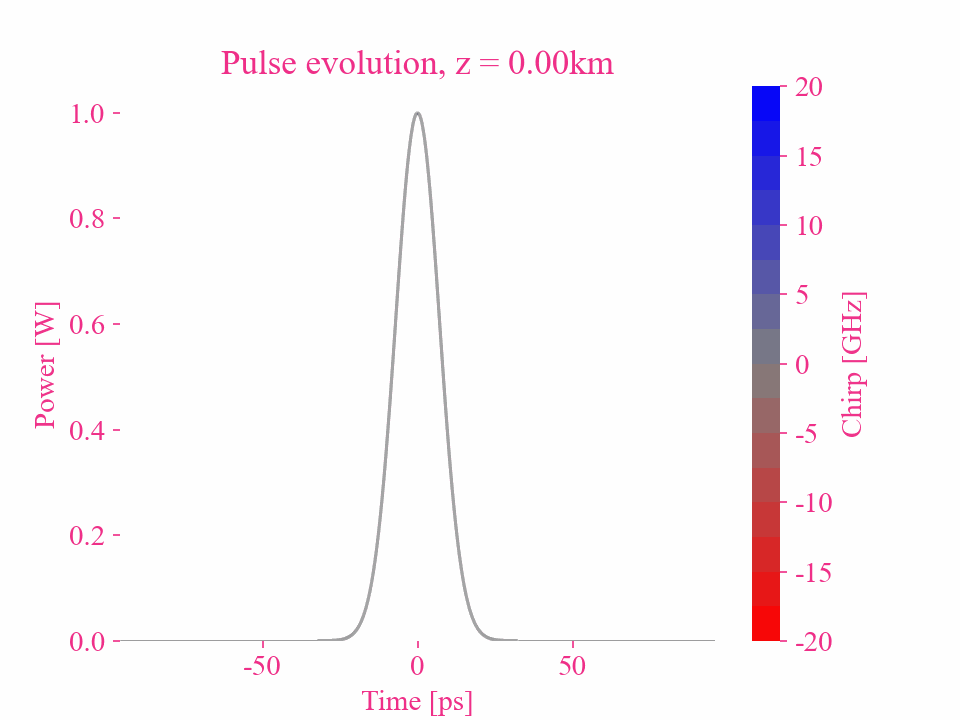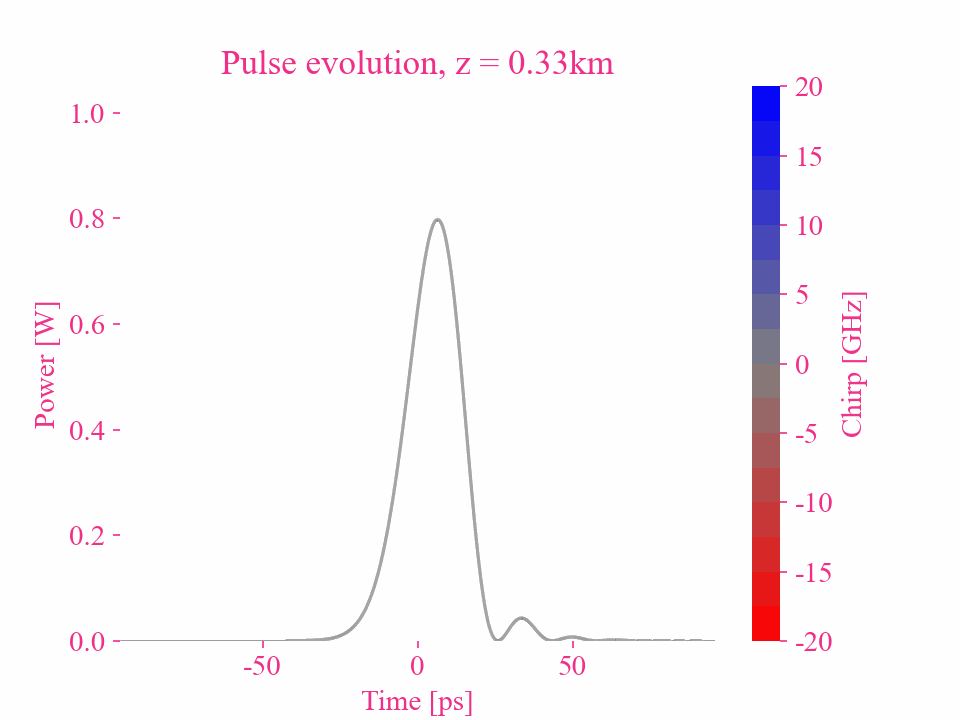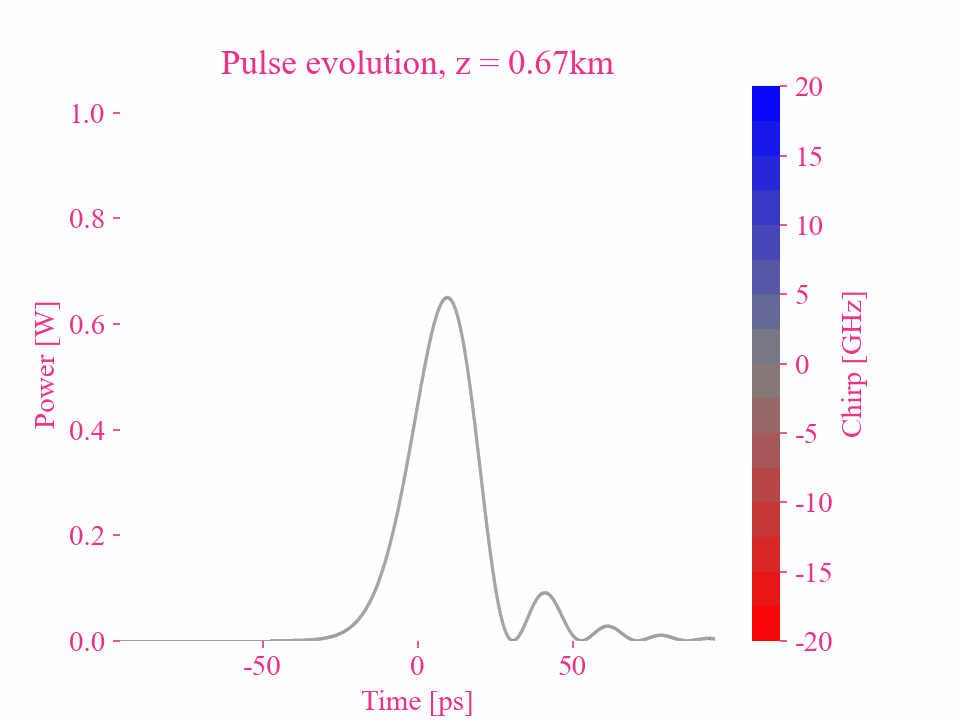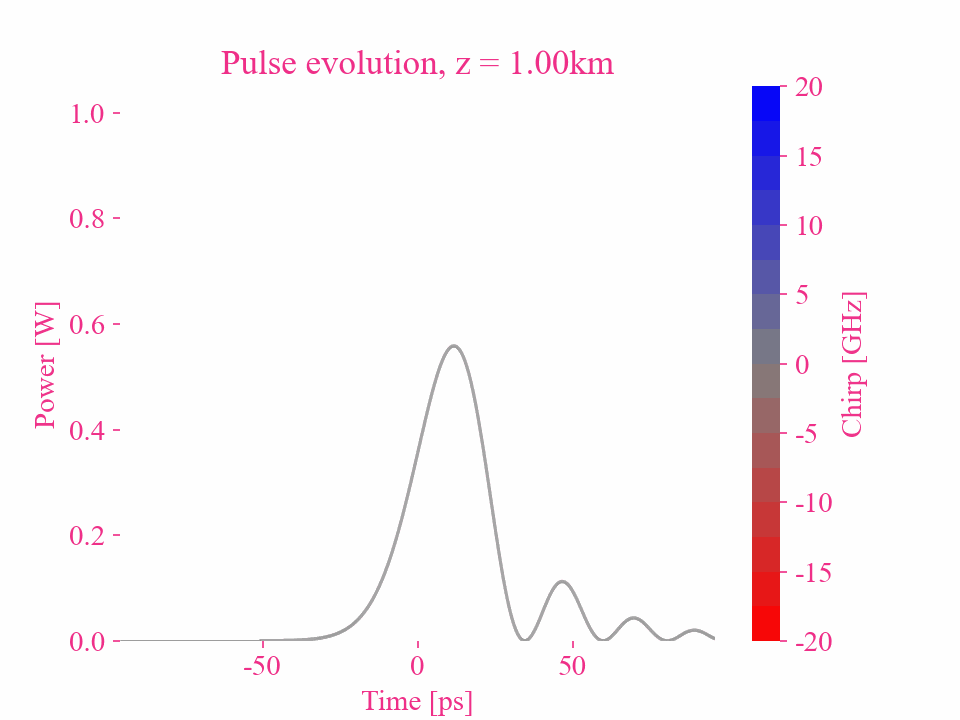
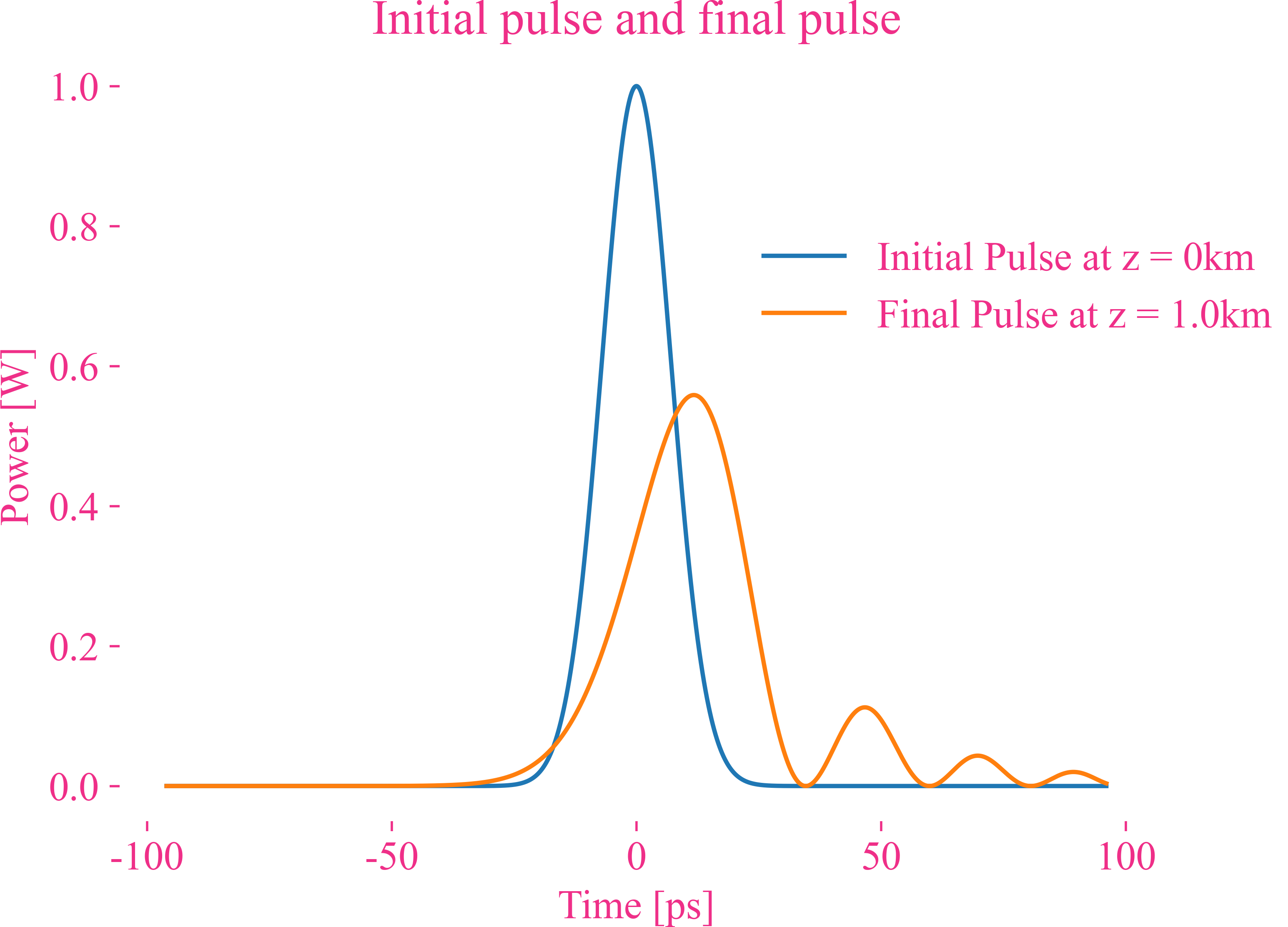
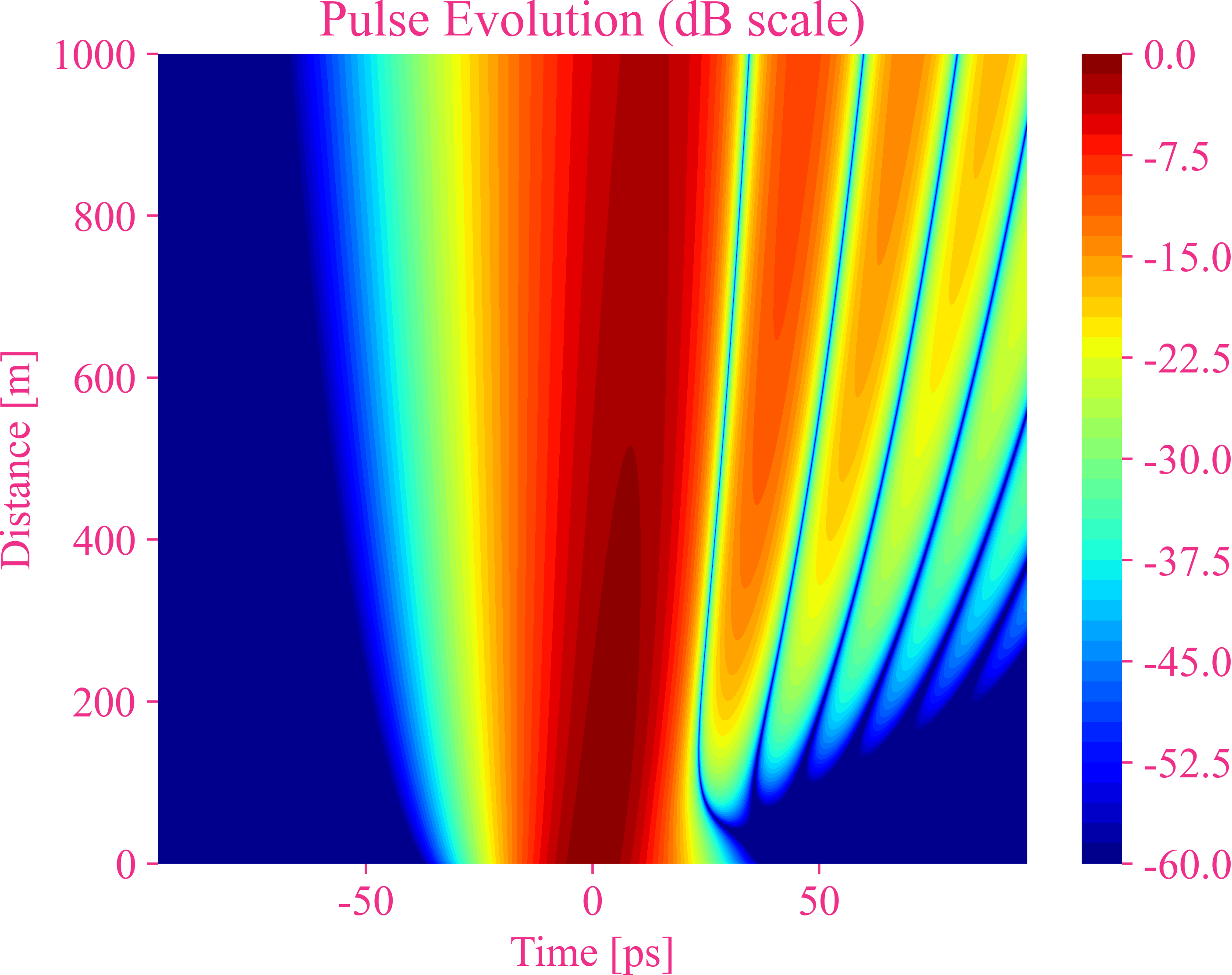
高斯脉冲的更高阶色散
四阶色散
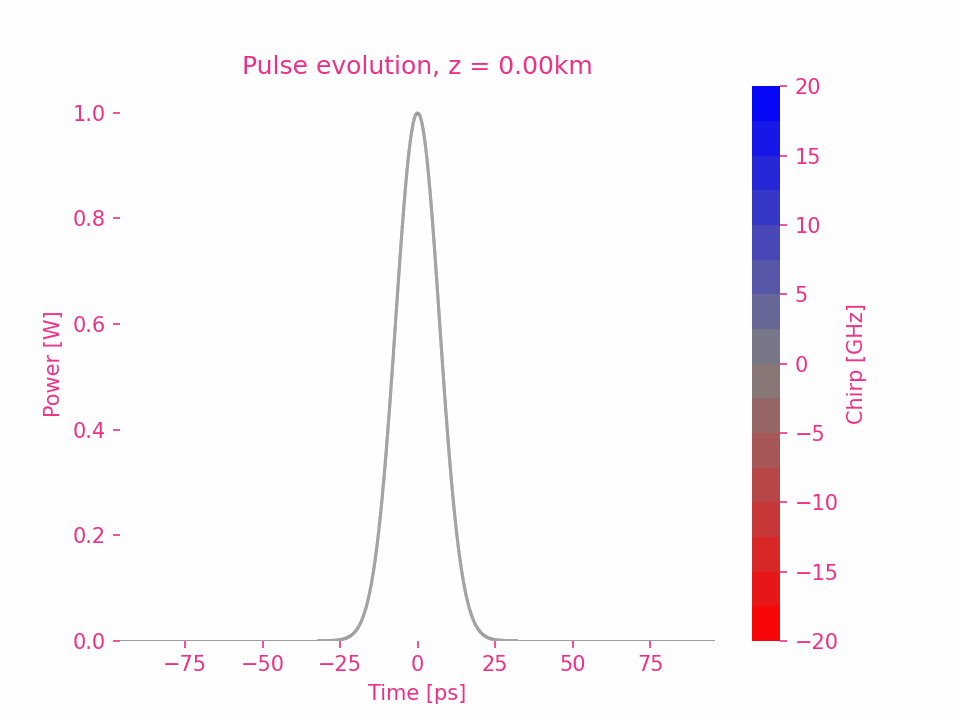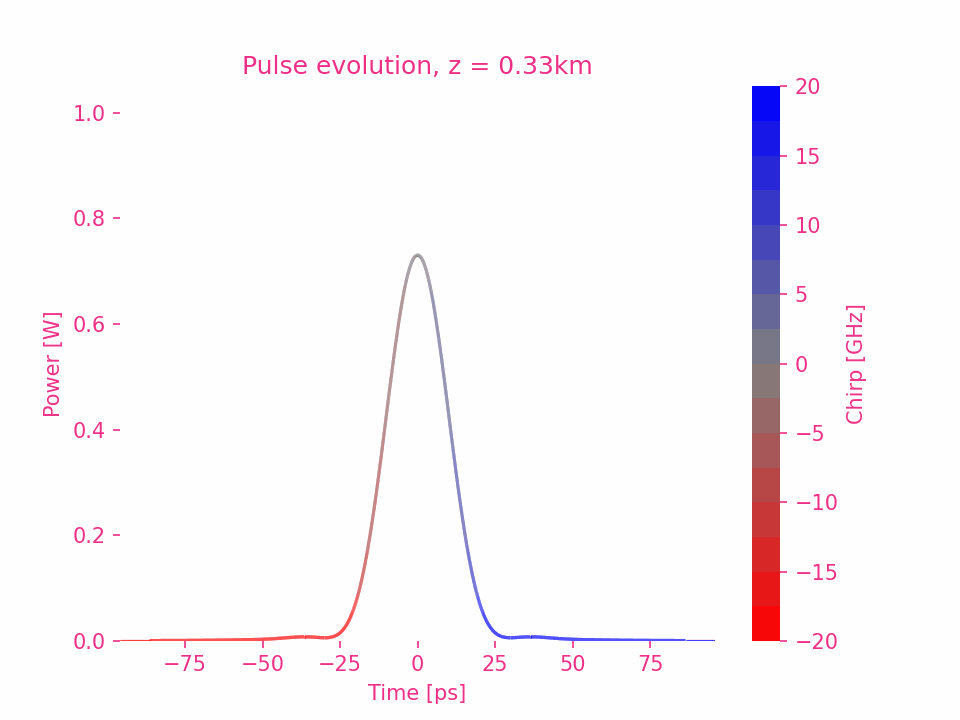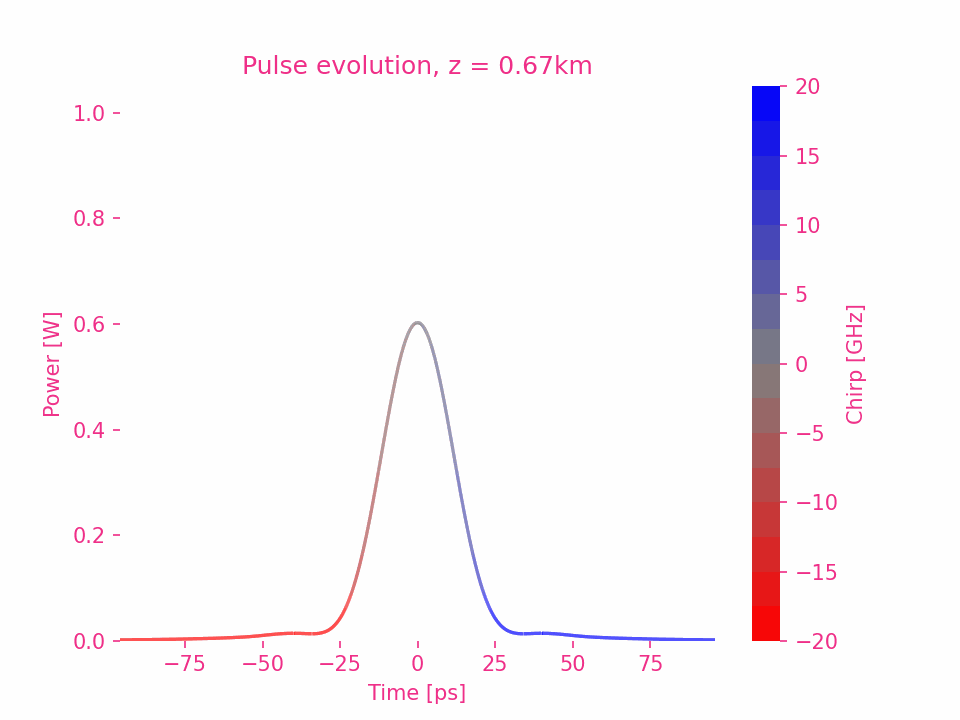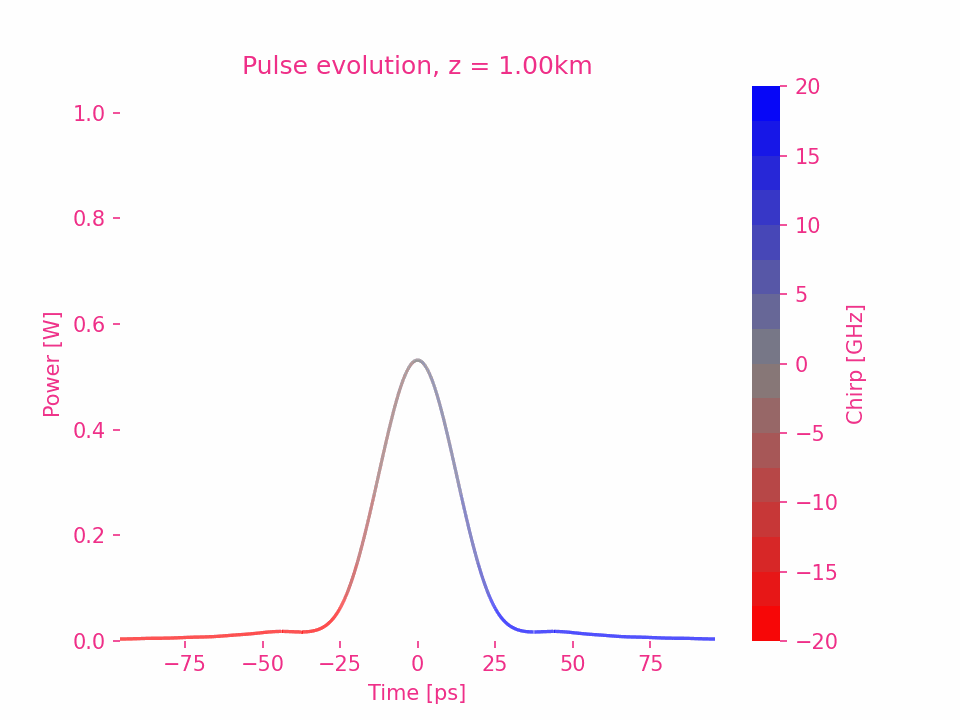
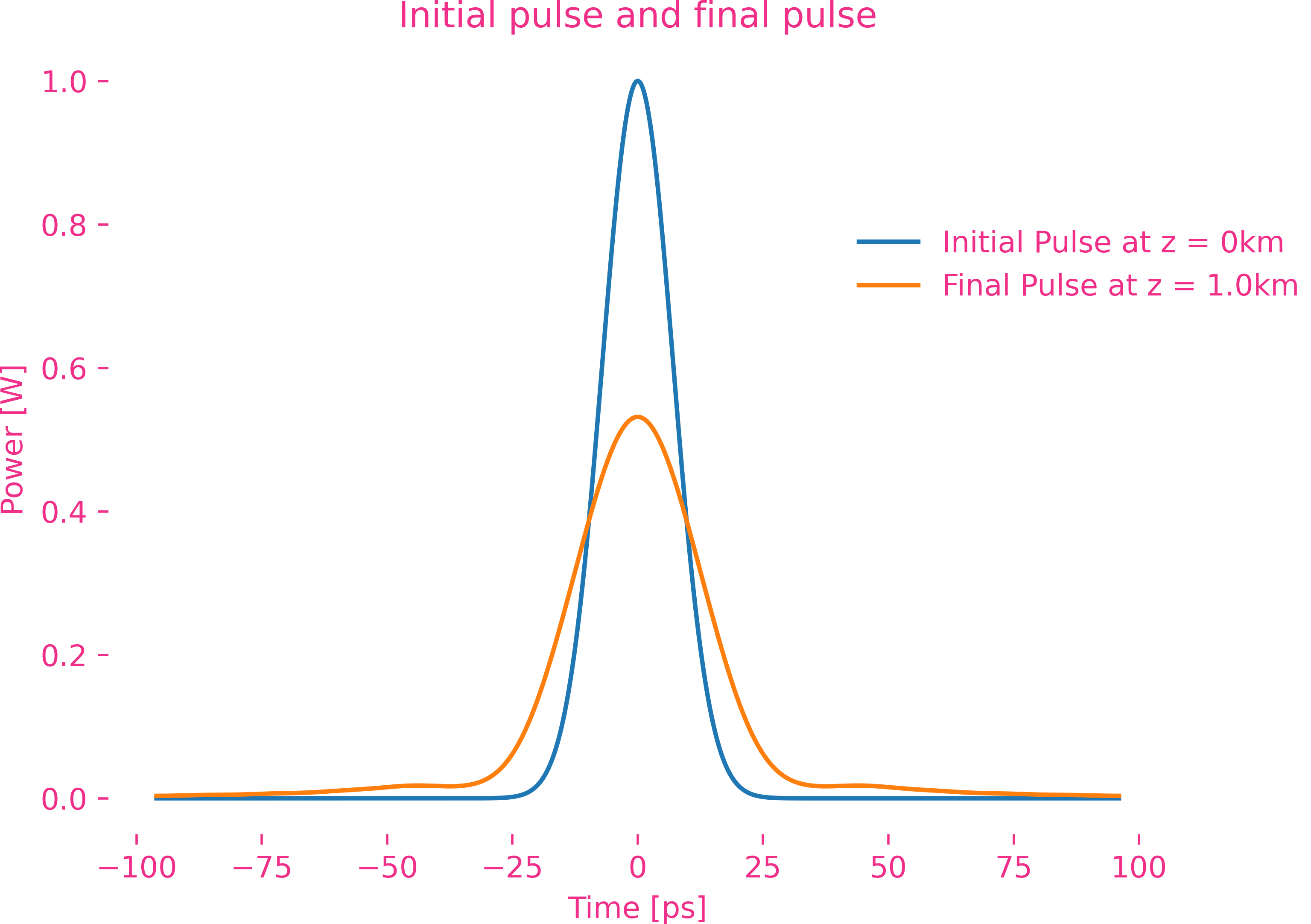
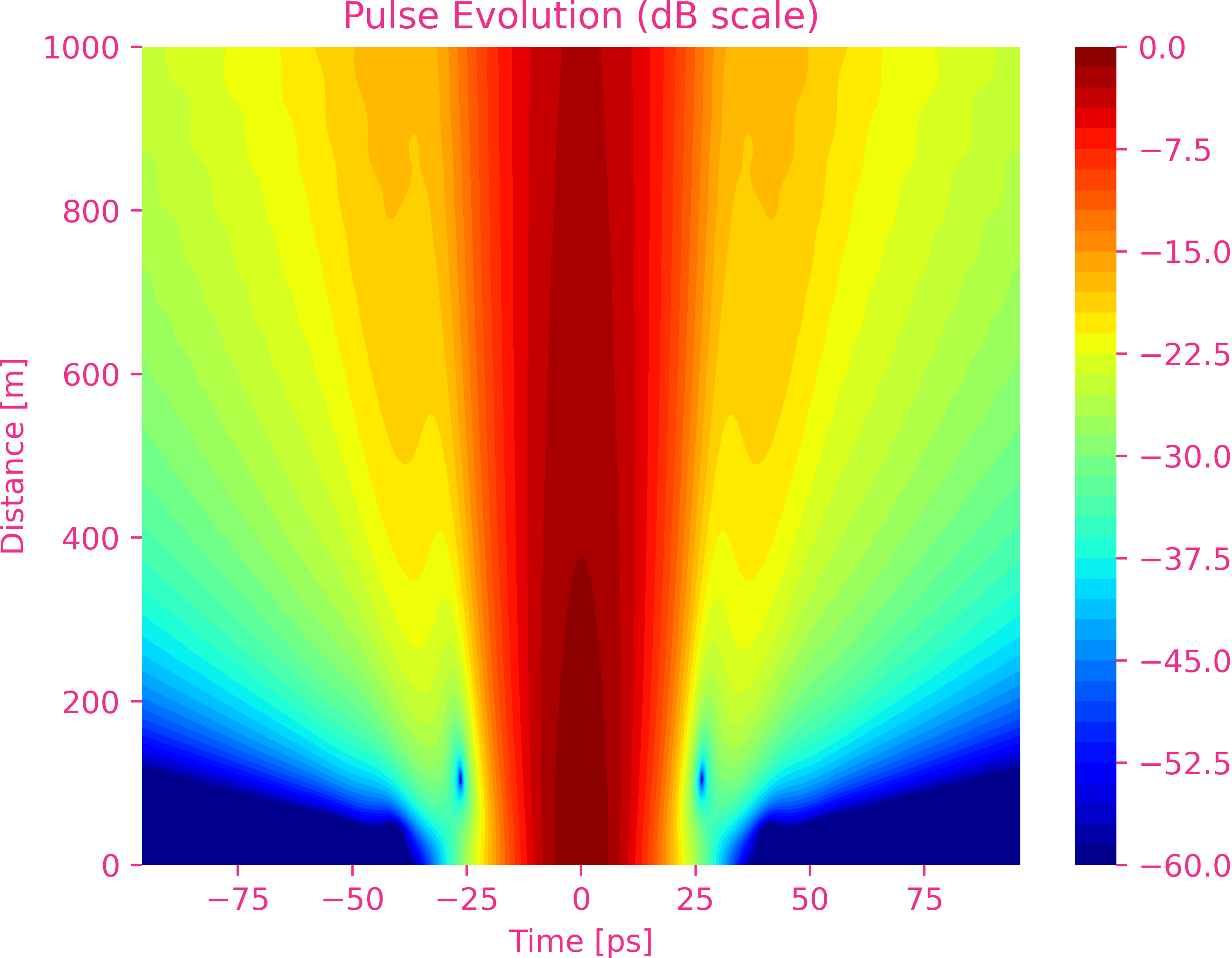
五阶色散
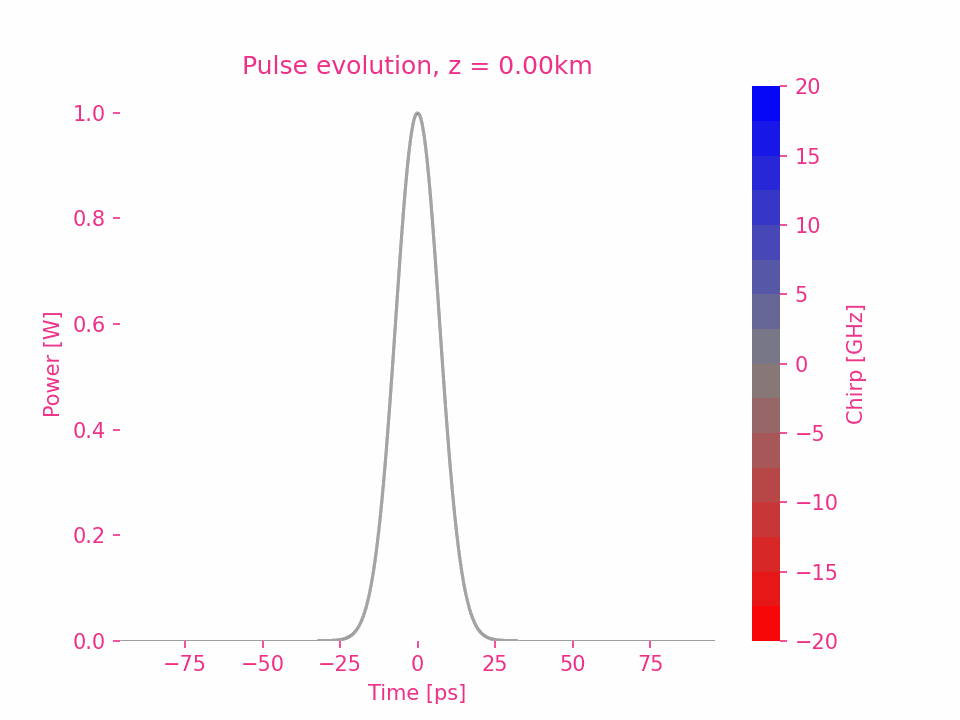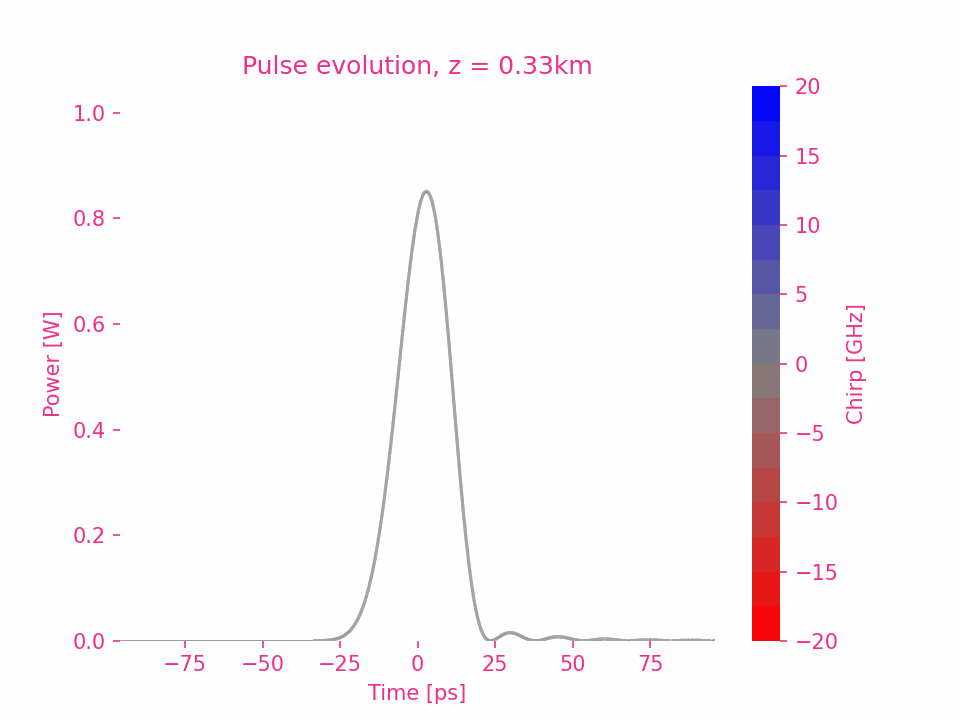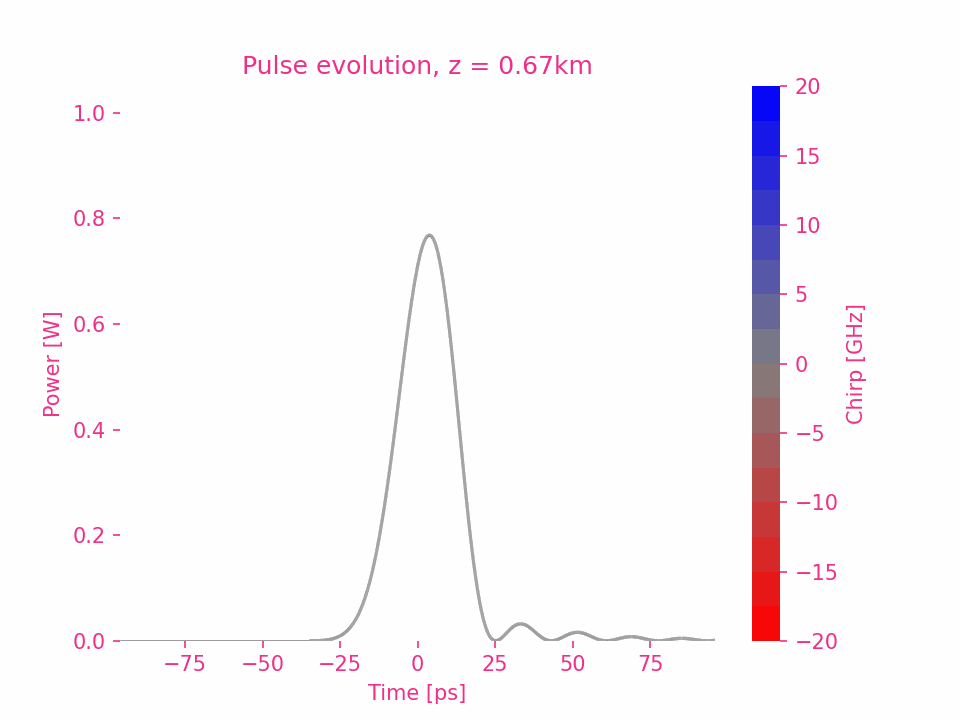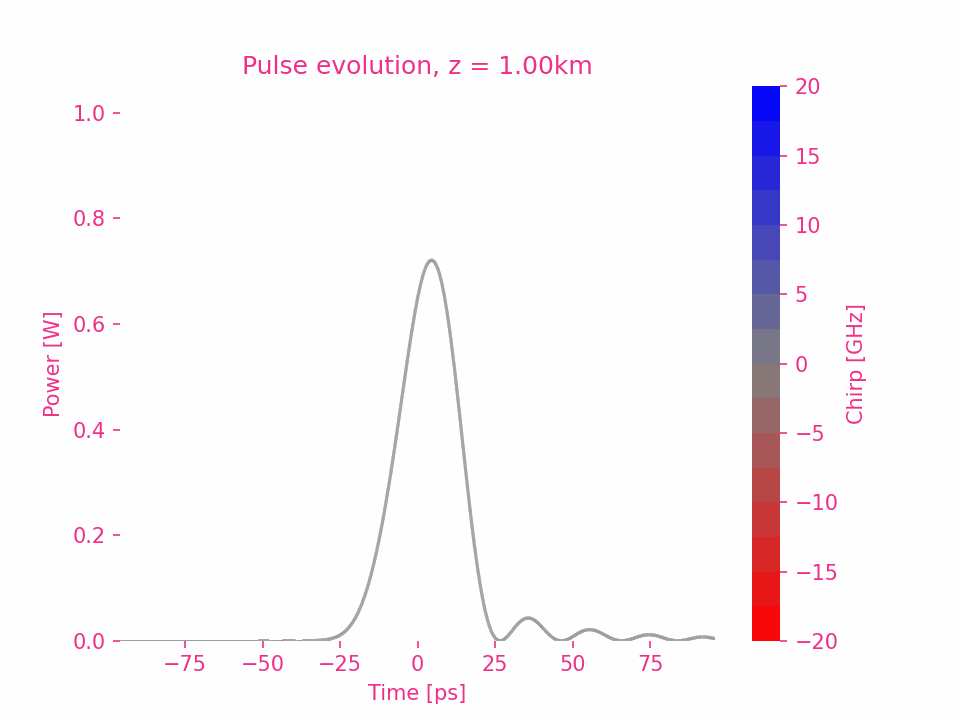
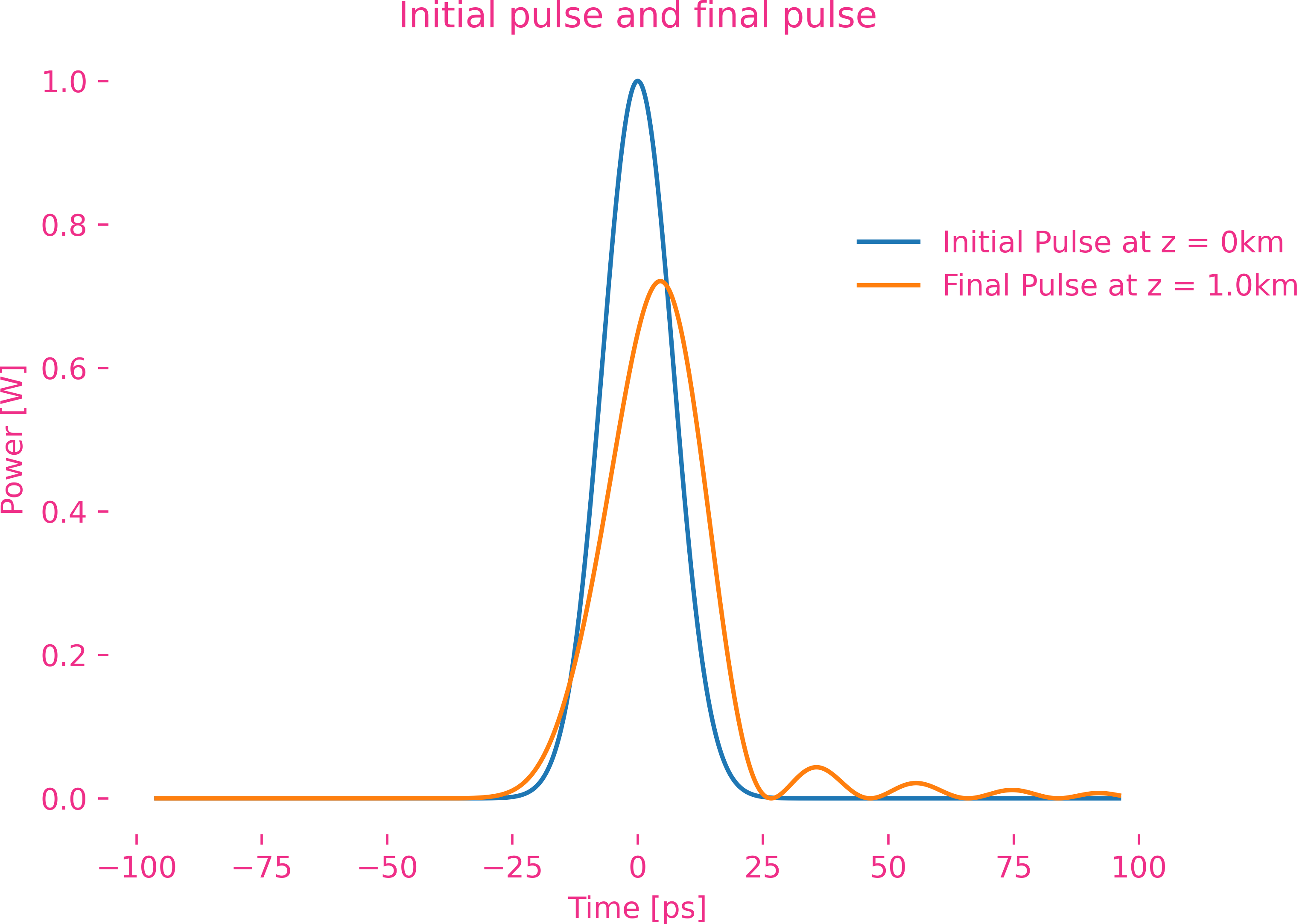
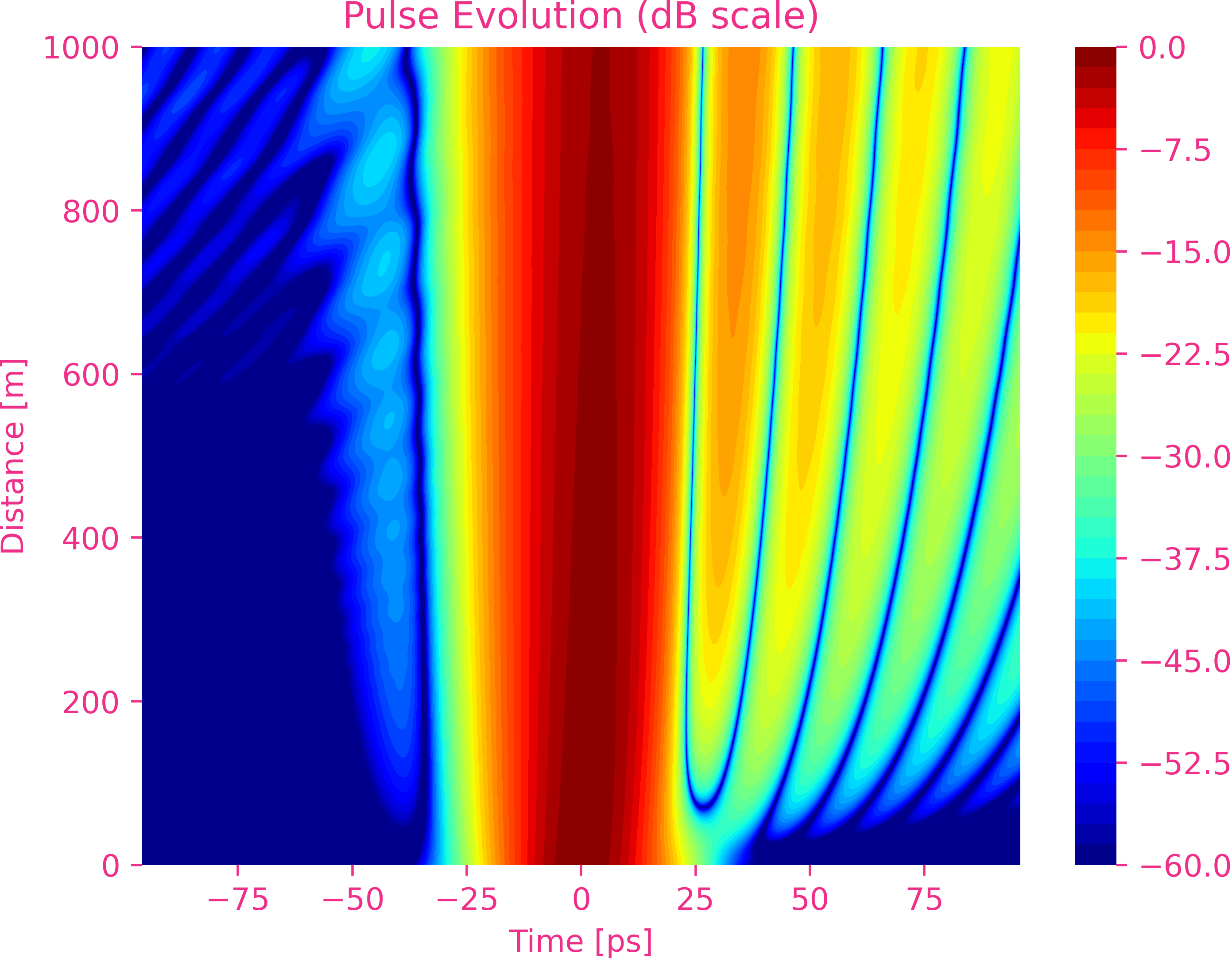
六阶色散
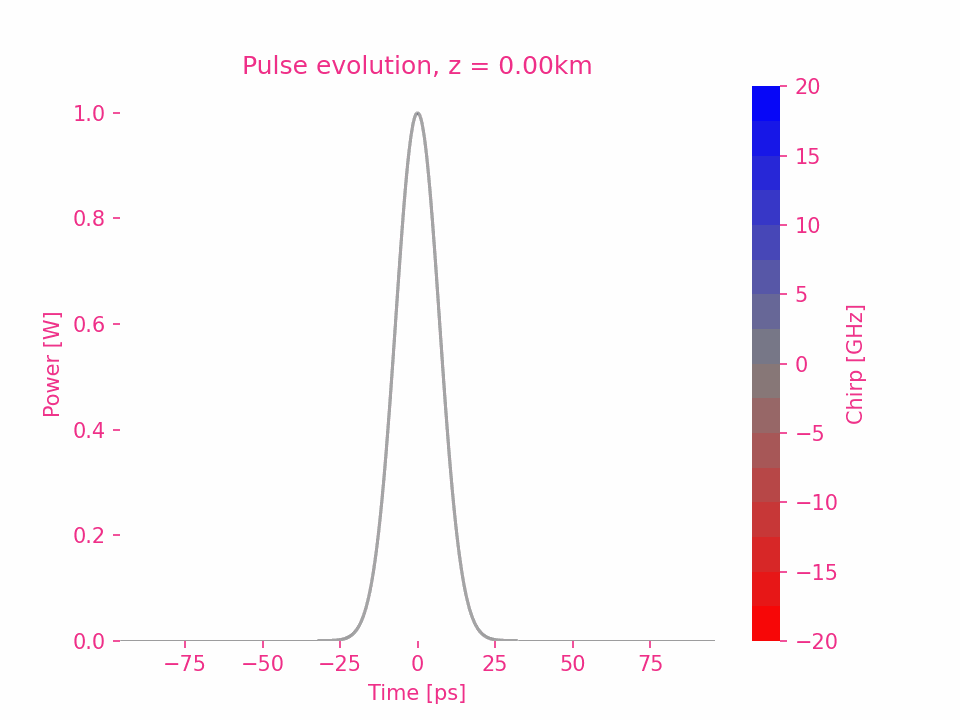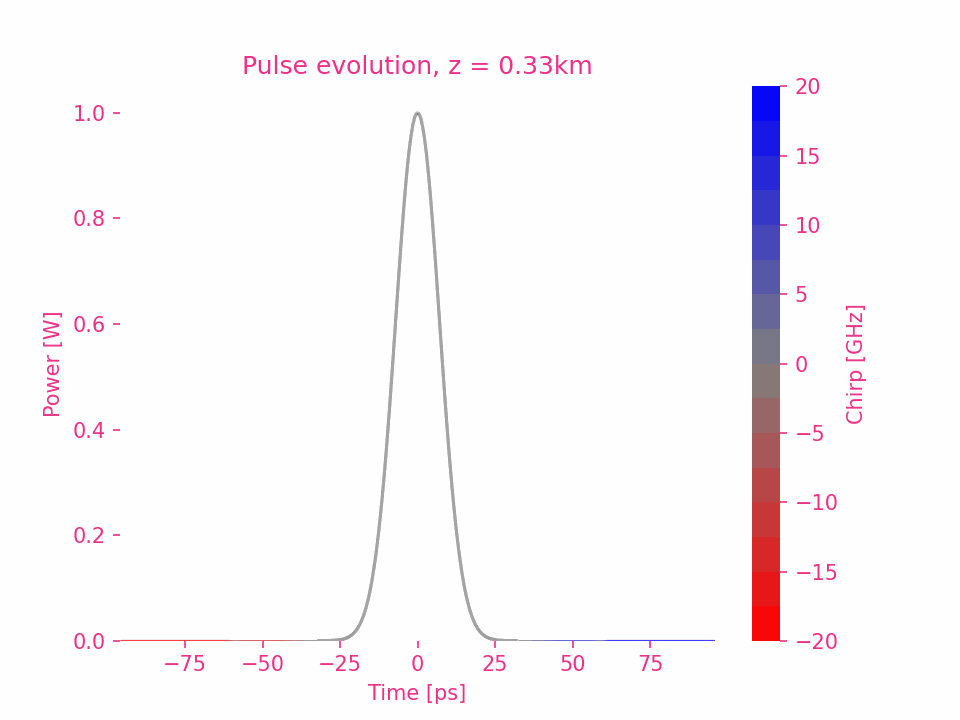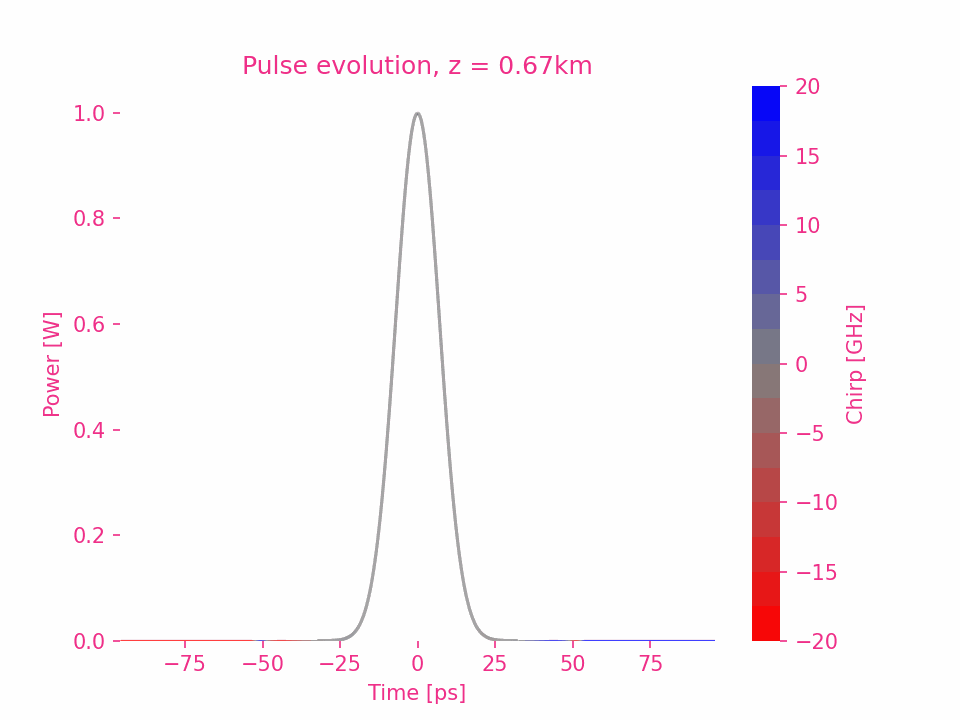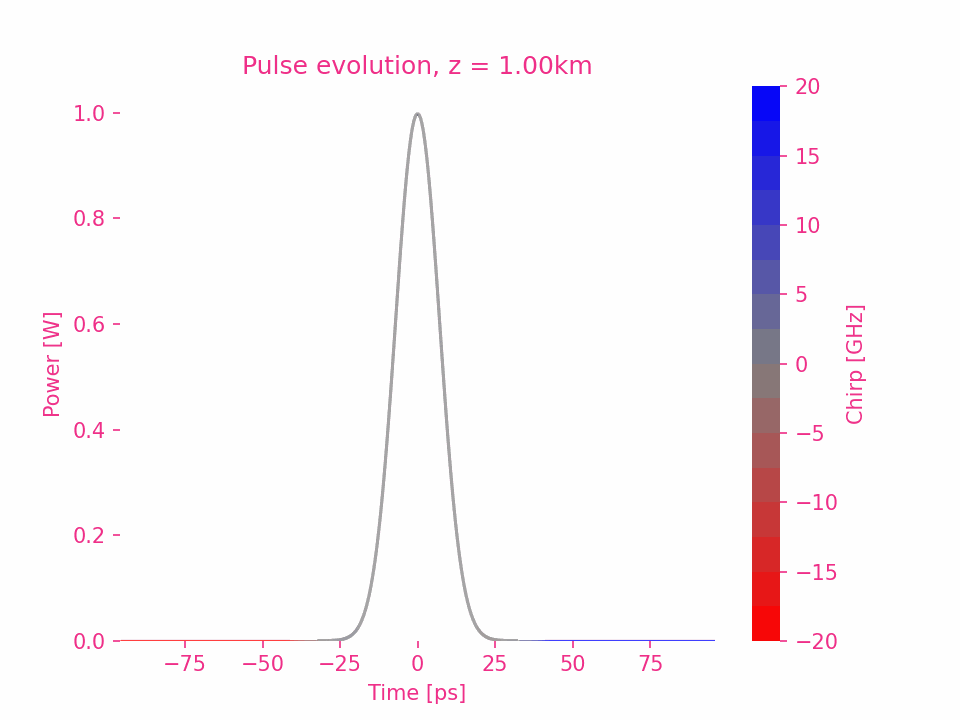
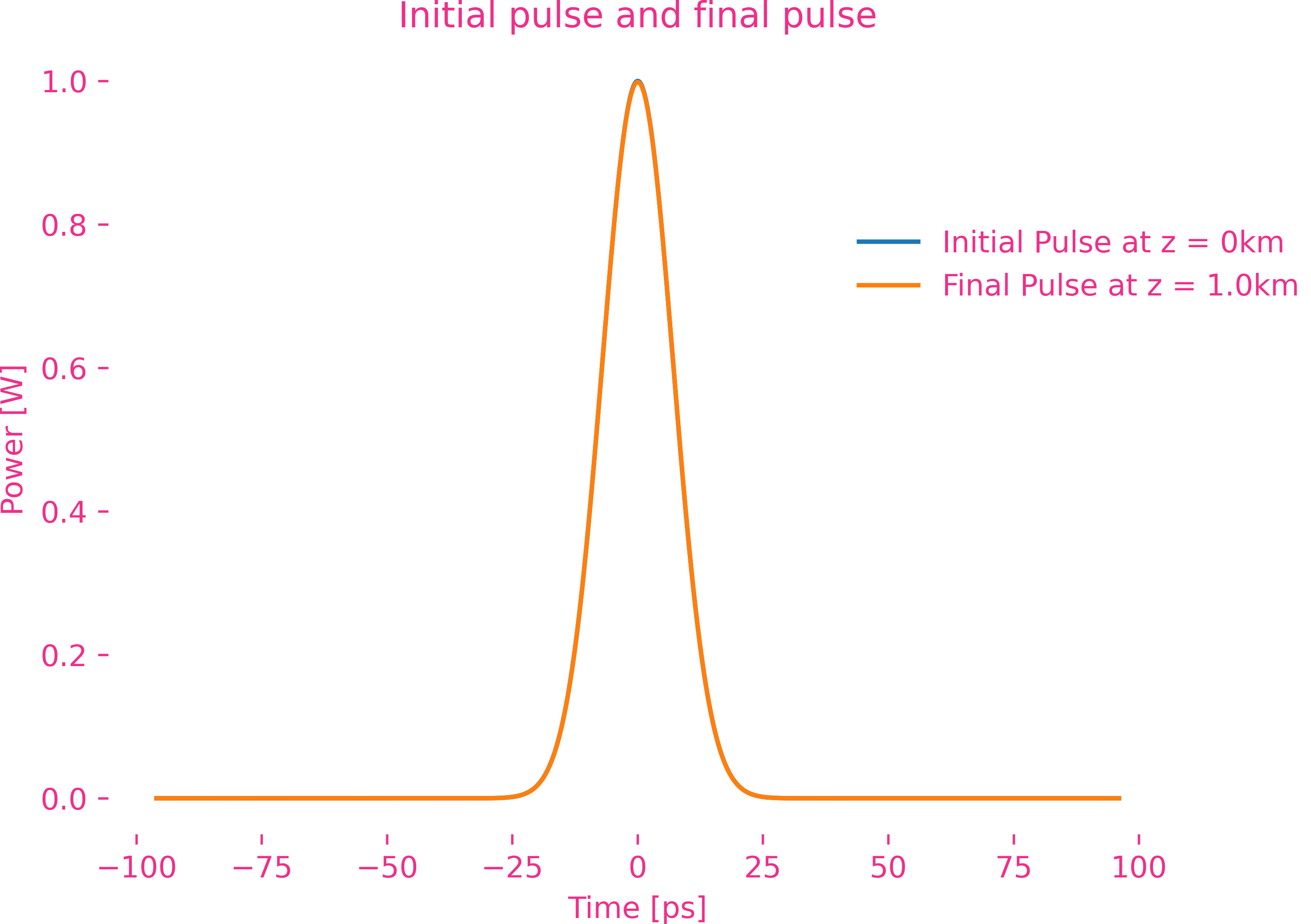
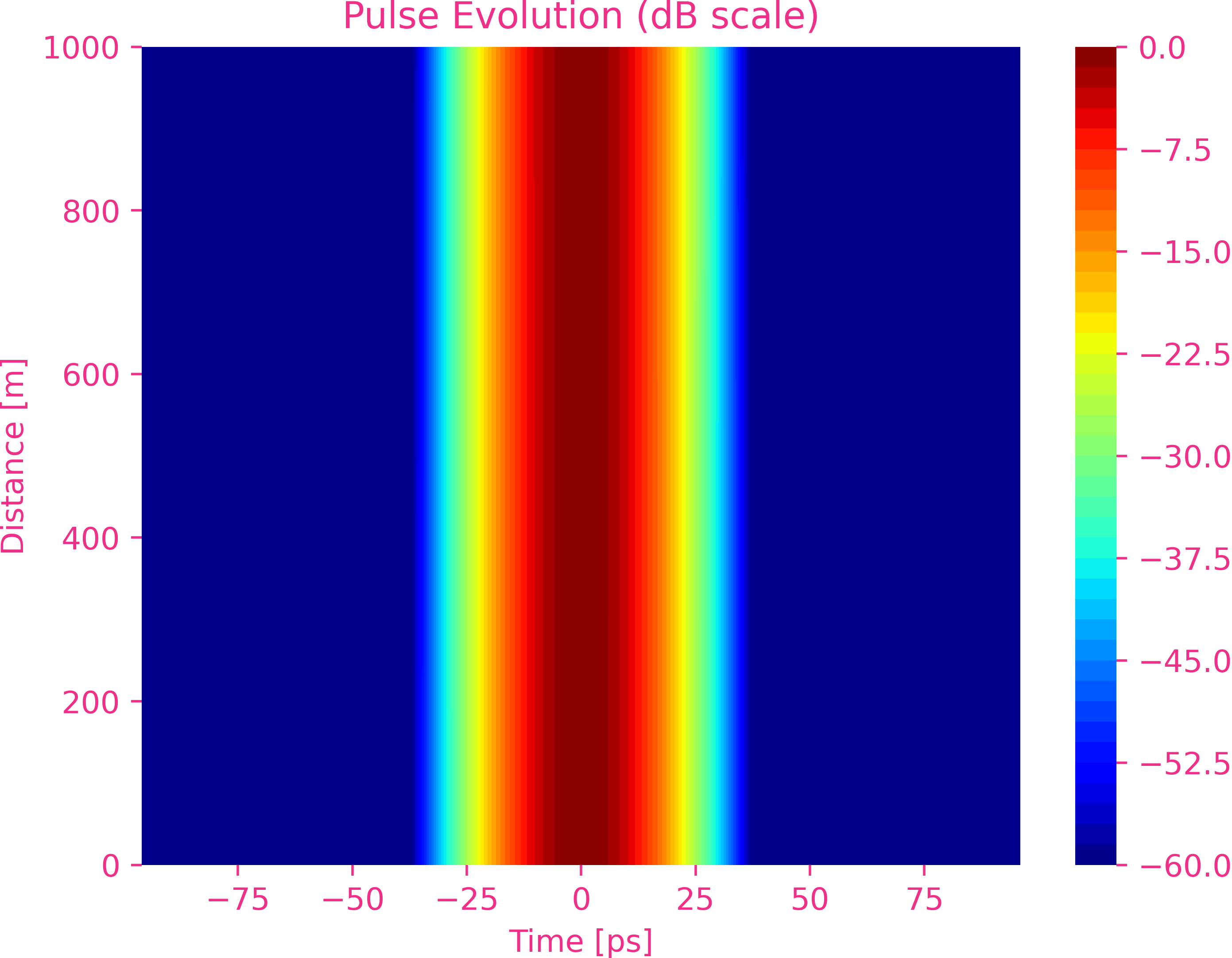
To be continue…
啁啾高斯脉冲
双曲正割脉冲
超高斯脉冲
深入理解高阶色散