Understanding High Order Dispersion
This article contains multiple .GIF images, which may slow down the webpage loading speed.
When considering the influence of high-order dispersion on pulse transmission, the attenuation $\alpha$ and non-linear parameter $\gamma$ in the pulse transmission equation are usually simplified as 0 for convenience. At the same time, the pulse intensity $A$ is normalized to $U$.
The normalized pulse satisfies in the time domain:
$$
\mathrm{i}\frac{\partial U}{\partial z}=\frac{\beta_2}{2}\frac{\partial^2U}{\partial T^2}+\mathrm{i}\frac{\beta_3}{6}\frac{\partial^3U}{\partial T^3}+…
$$
In the frequency domain, it becomes:
$$
\frac{\partial U}{\partial z}=\mathrm{i}[\frac{\beta_2}{2}(\omega-\omega_0)^2+\frac{\beta_3}{6}(\omega-\omega_0)^3+…]\widetilde U
$$
It shows that when the optical pulse is transmitted through the optical fiber, each spectral component within its envelope undergoes a frequency-dependent phase shift.
The general solution of the equation in the frequency domain is:
$$
\widetilde{U}(z, \omega)=\widetilde{U}(0, \omega)\mathrm{e}^{\mathrm{i}\frac{\beta_2}{2}(\omega-\omega_0)^2z+\mathrm{i}\frac{\beta_3}{6}(\omega-\omega_0)^3z+…}
$$
Next, taking the Gaussian pulse as an example, we will separately analyze the impact of each order of dispersion on pulse transmission.
View the source code in my GitHub repository.
The group velocity dispersion of a Gaussian pulse
Taking $\beta_2>0$ as an example, the phase shift of each frequency component in the pulse is the square of the difference between the component frequency and the central frequency.
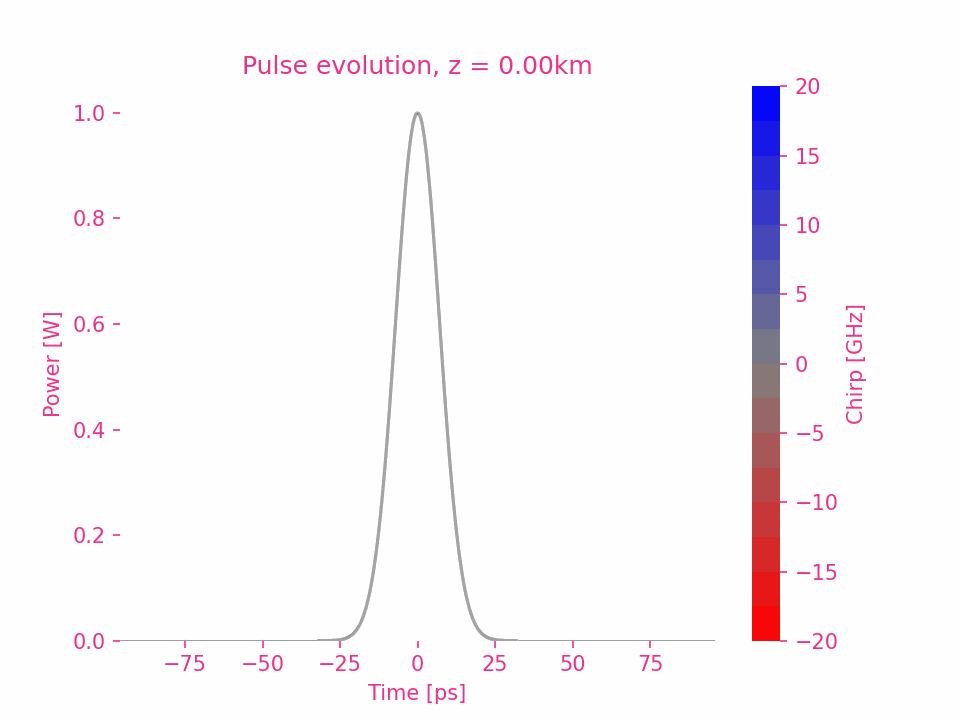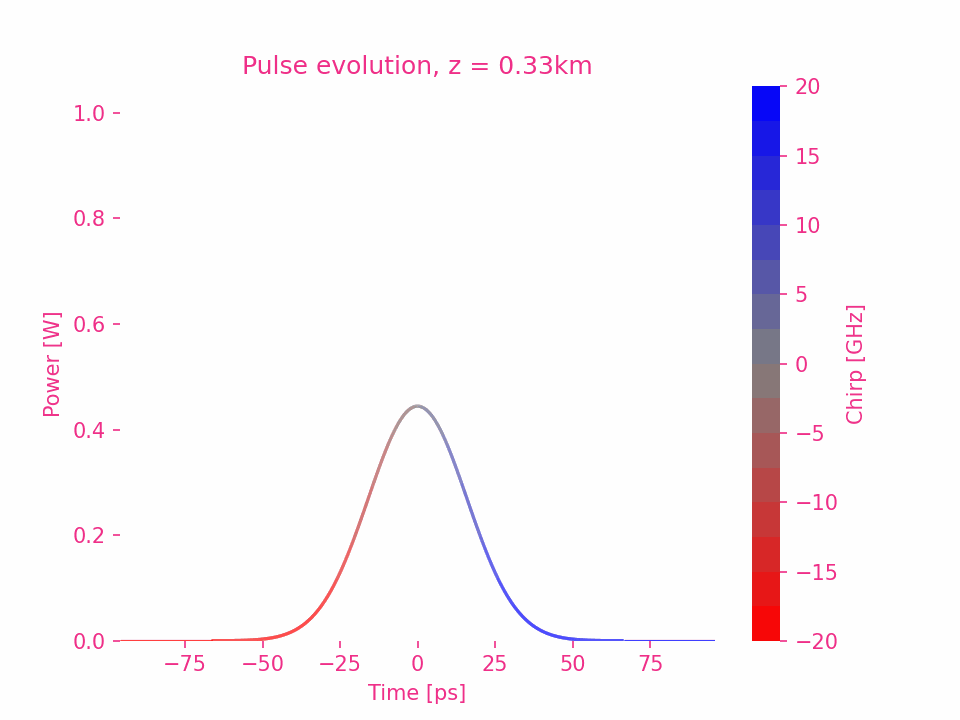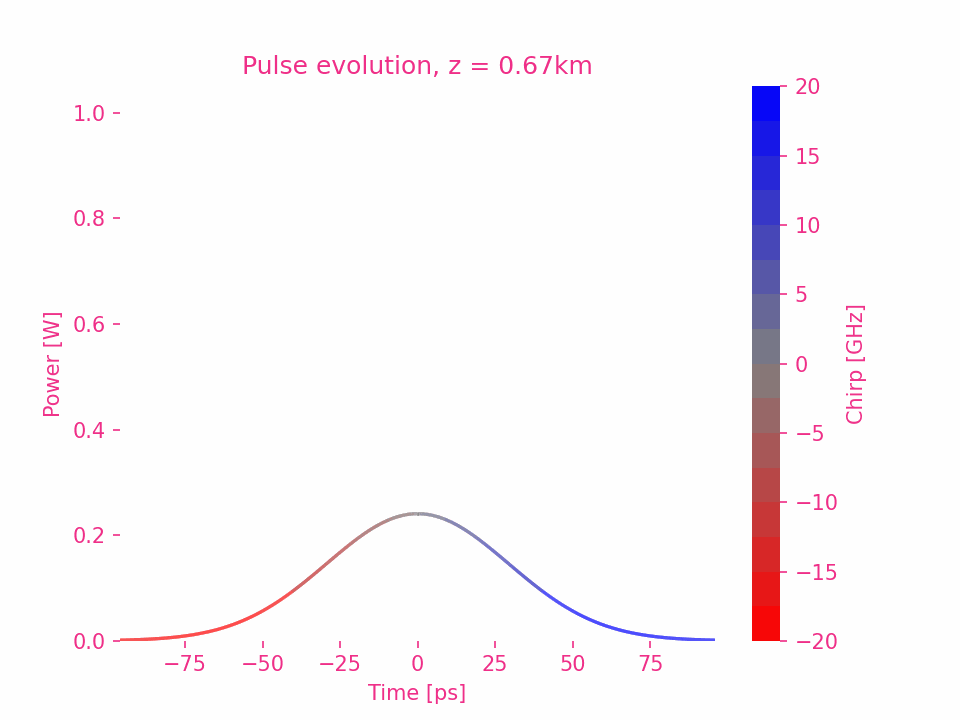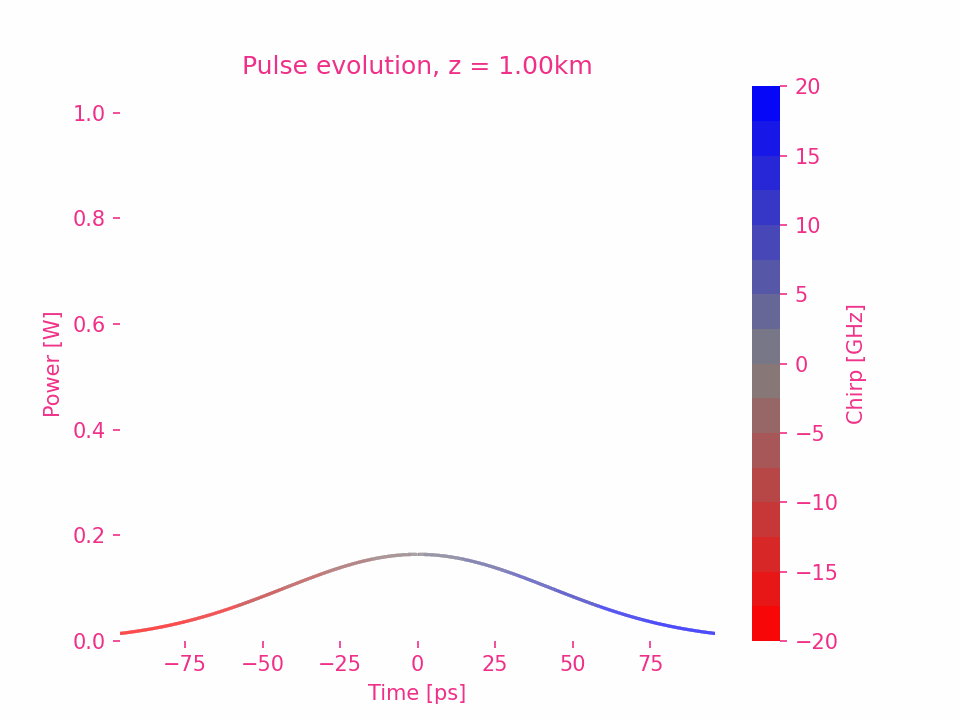
Third-order dispersion of a Gaussian pulse
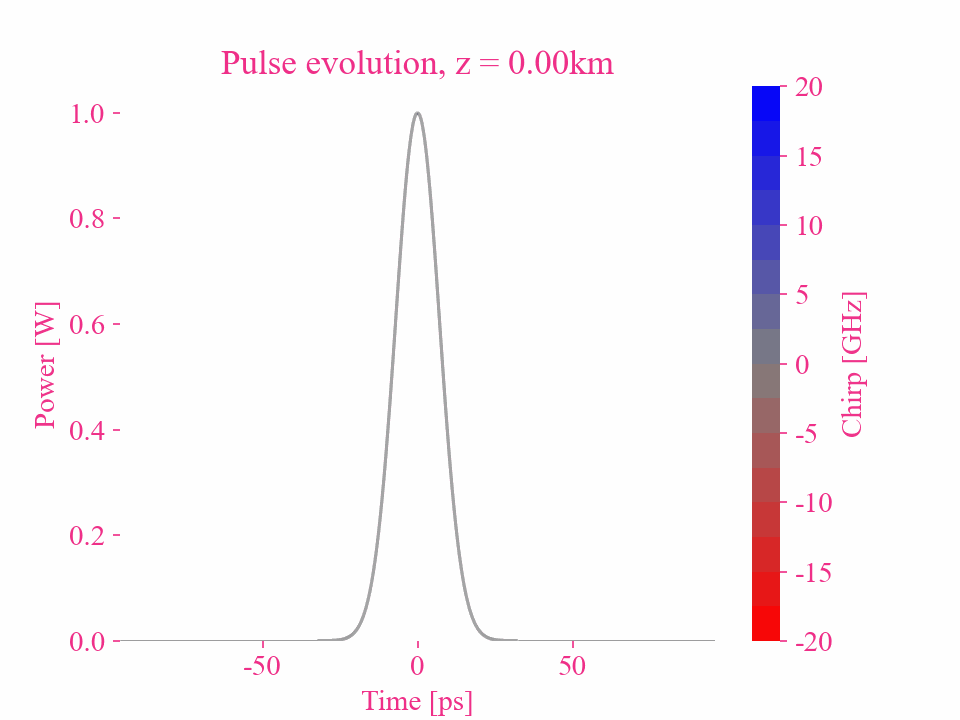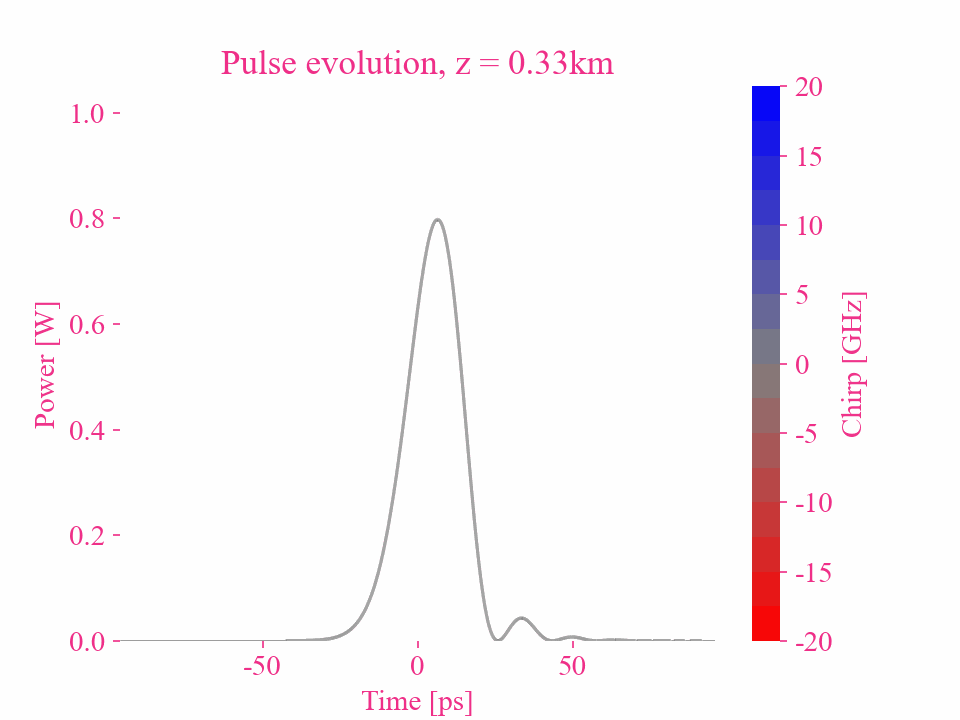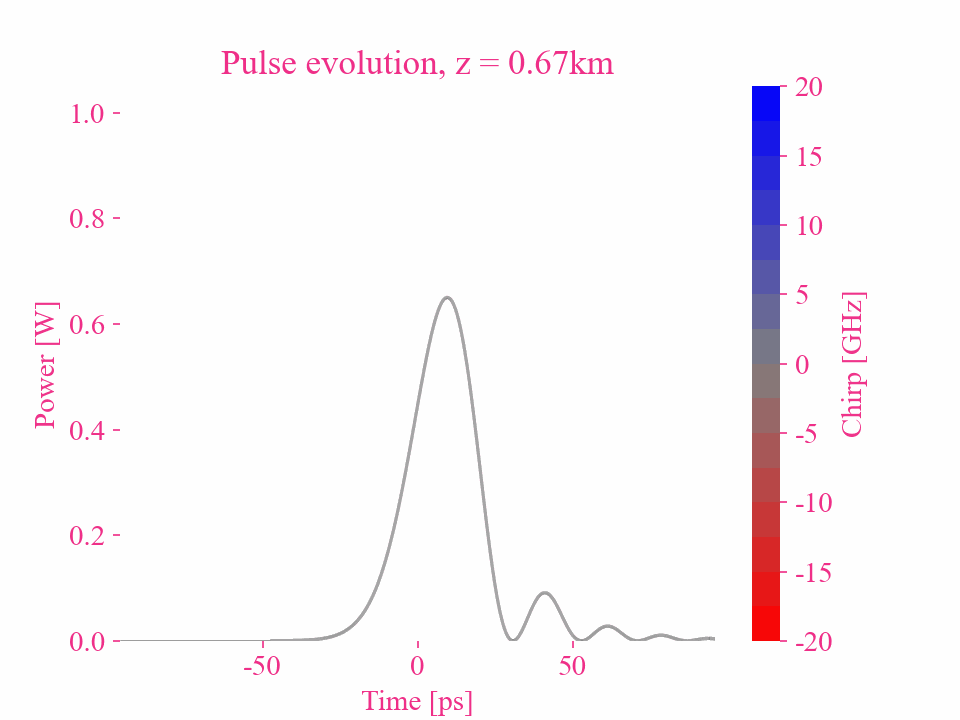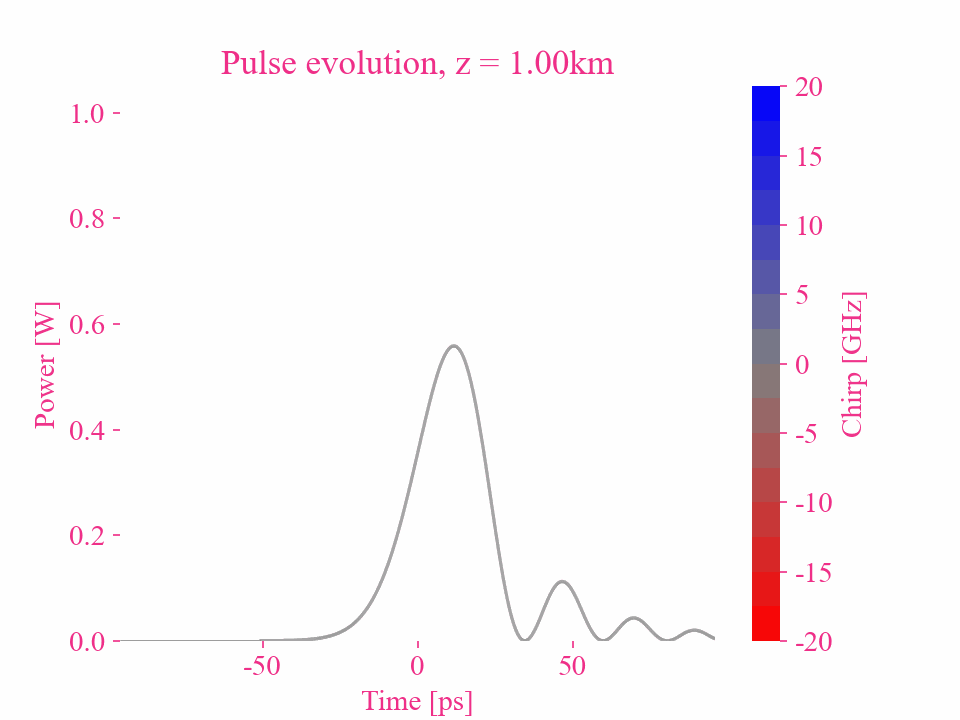
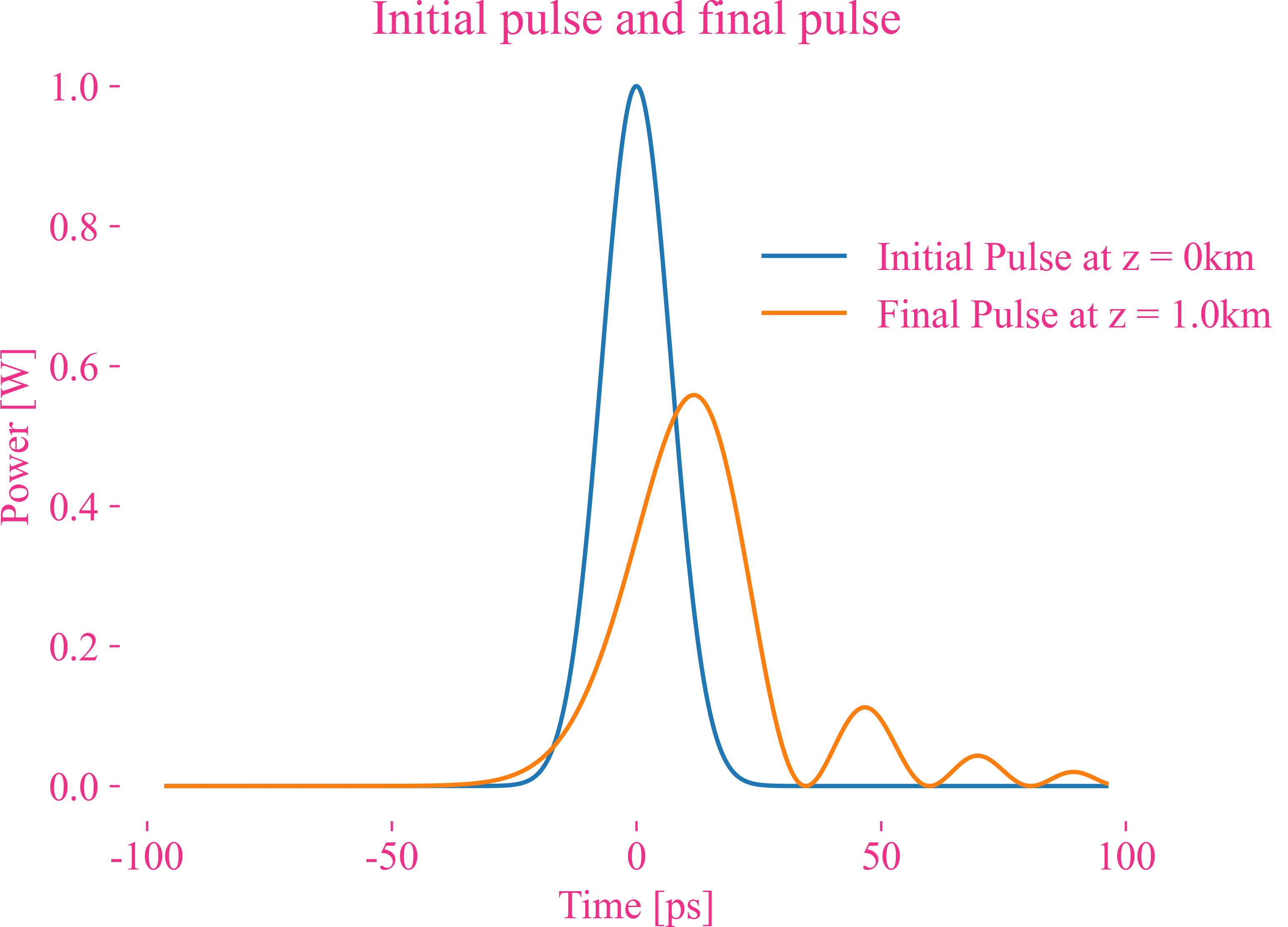
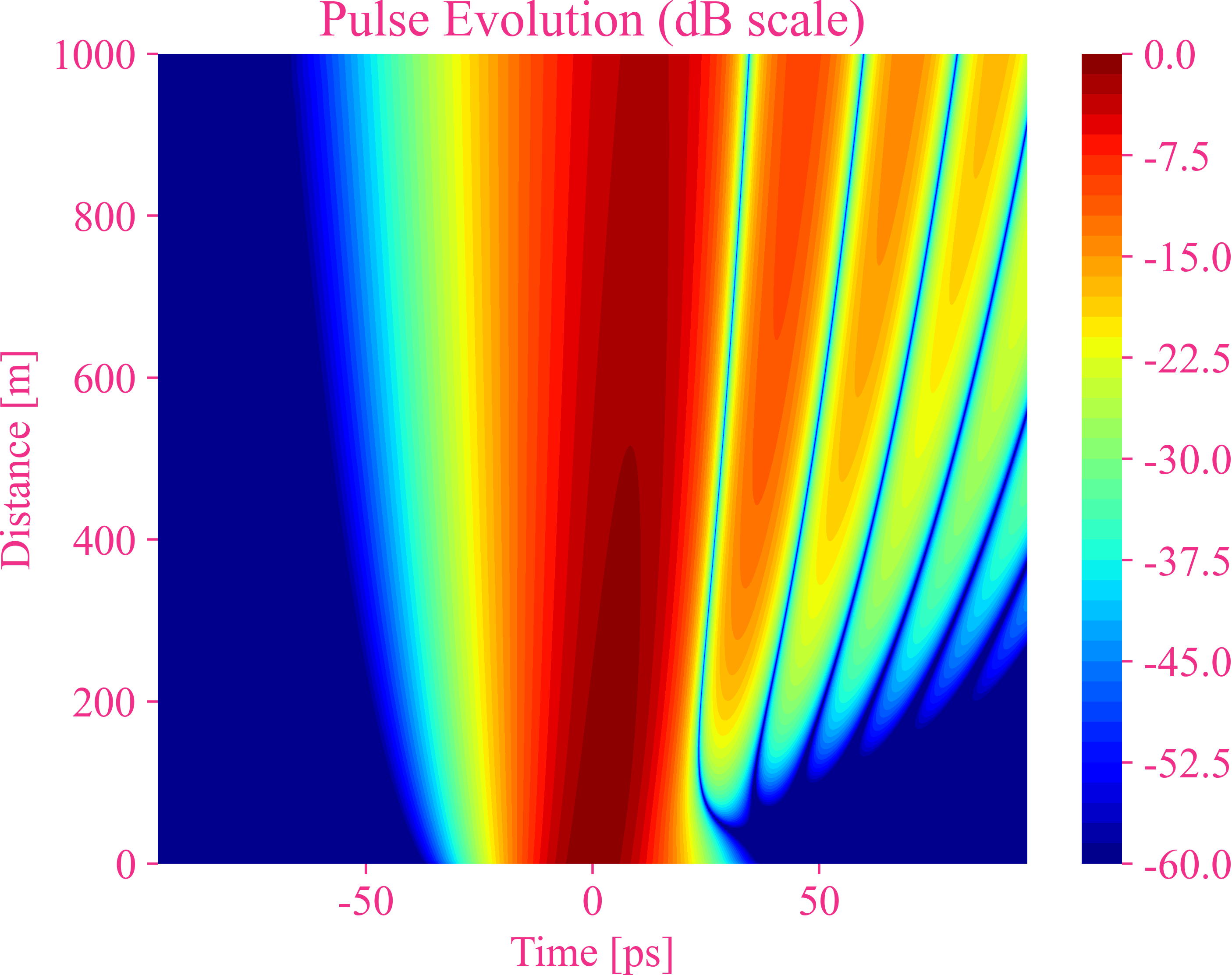
Higher-order dispersion of a Gaussian pulse
Fourth-order dispersion
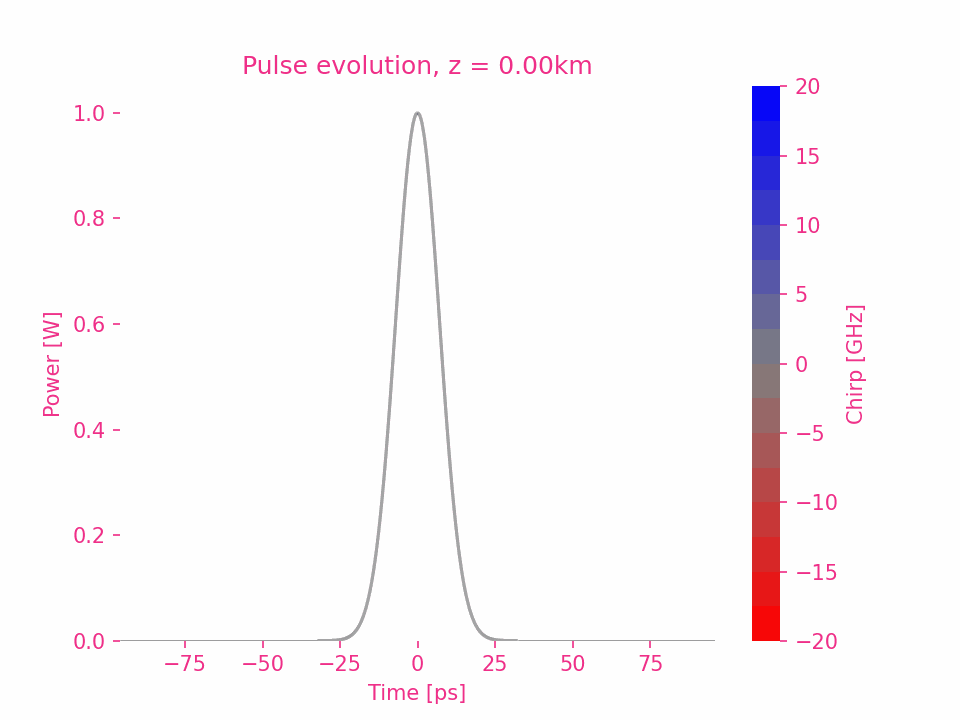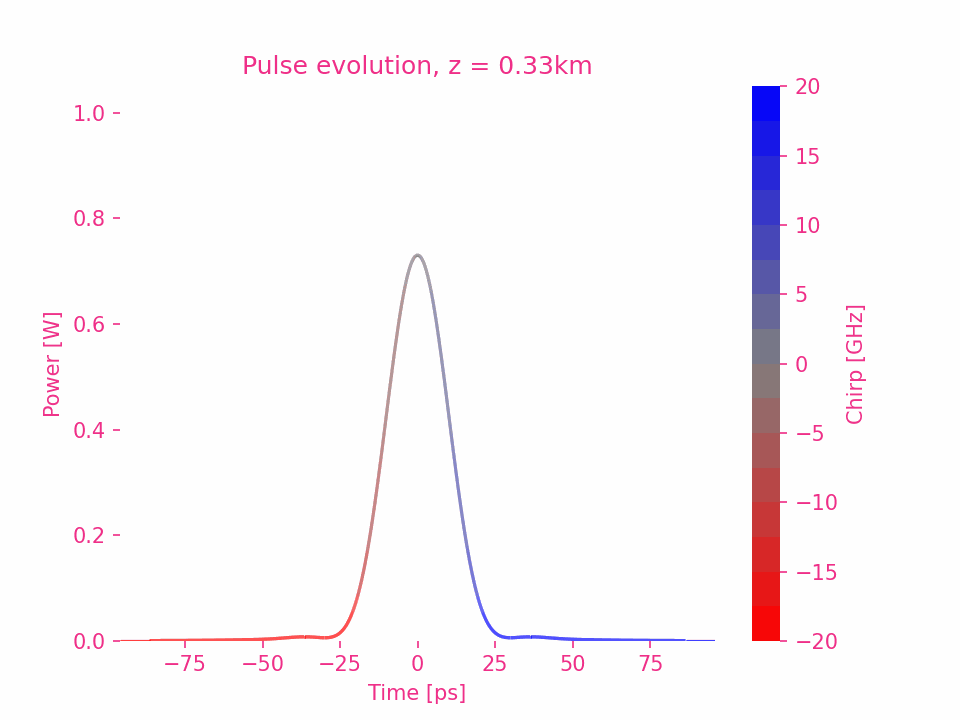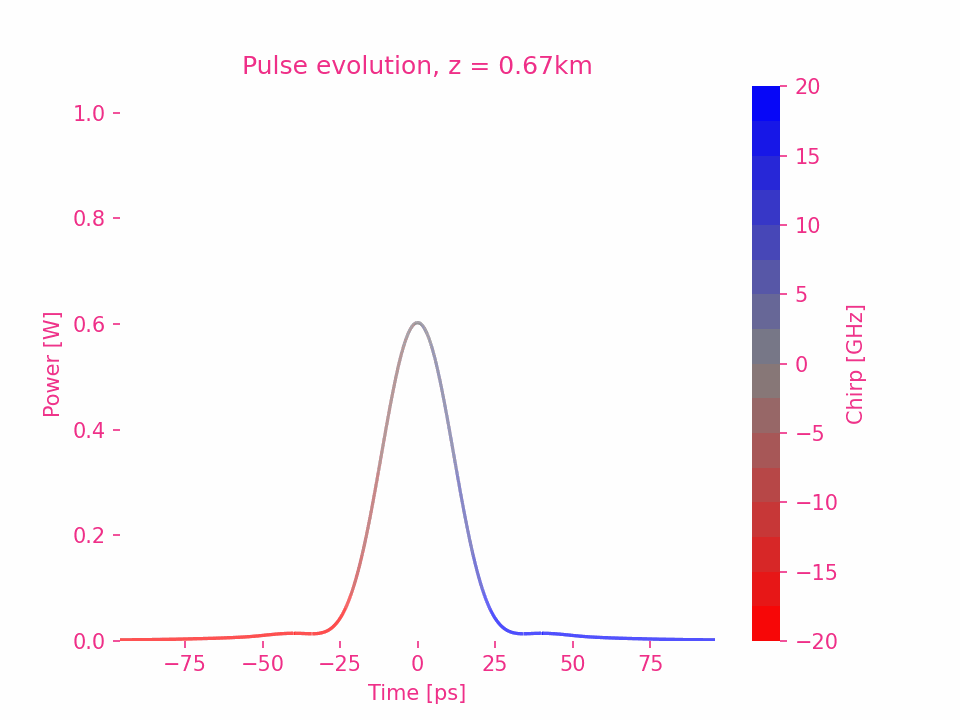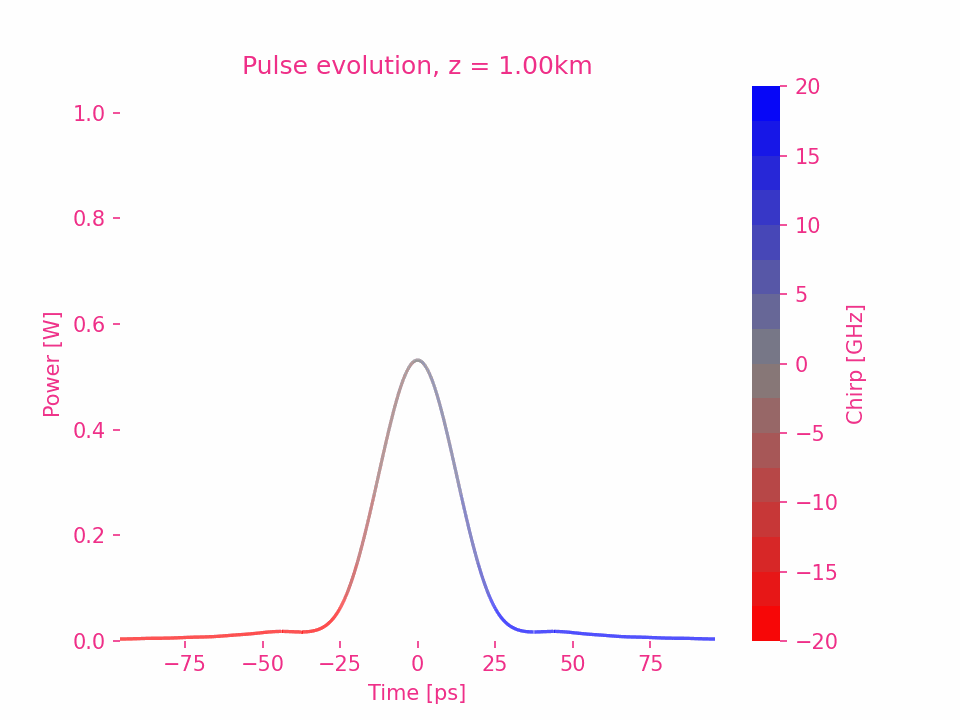
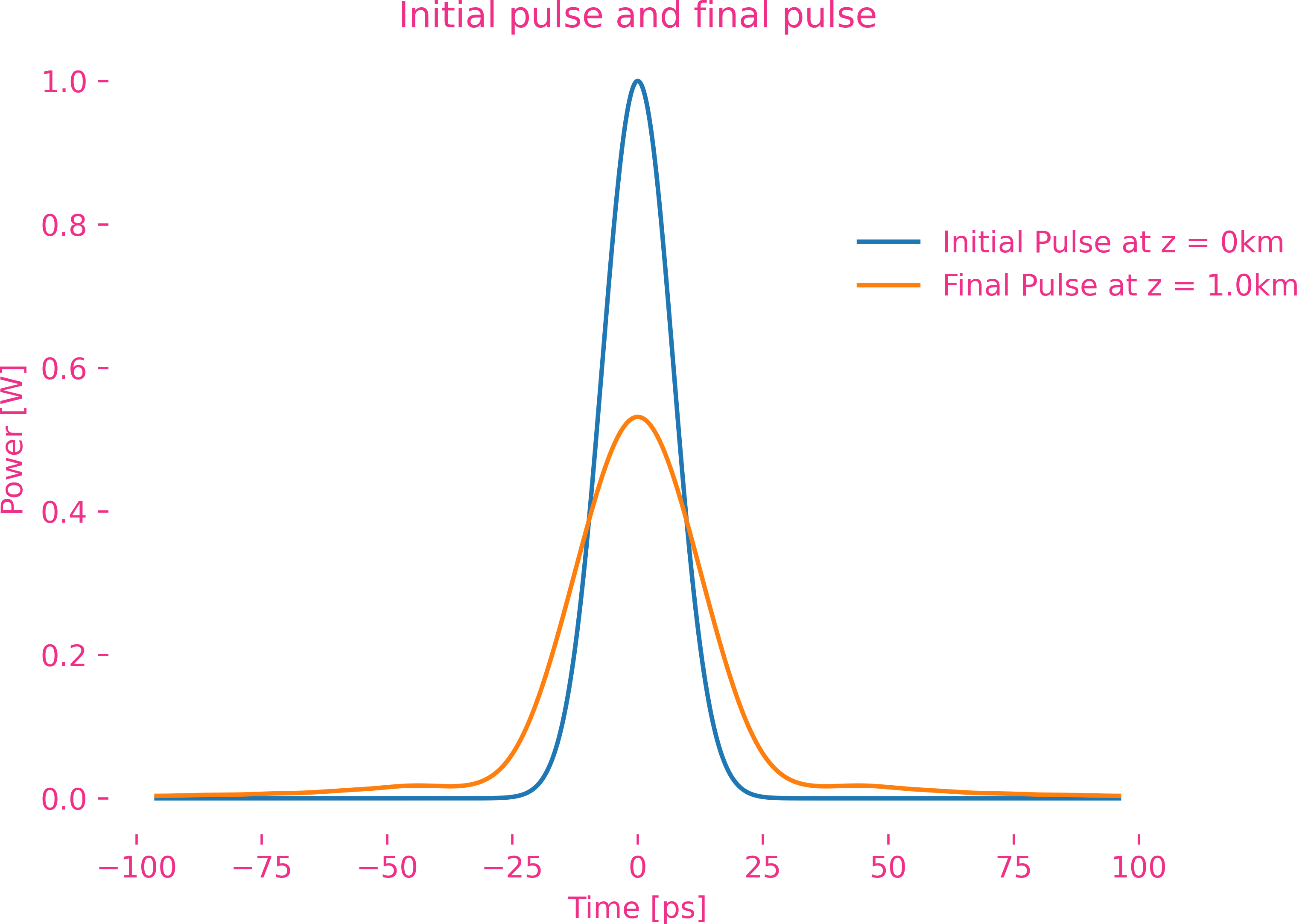
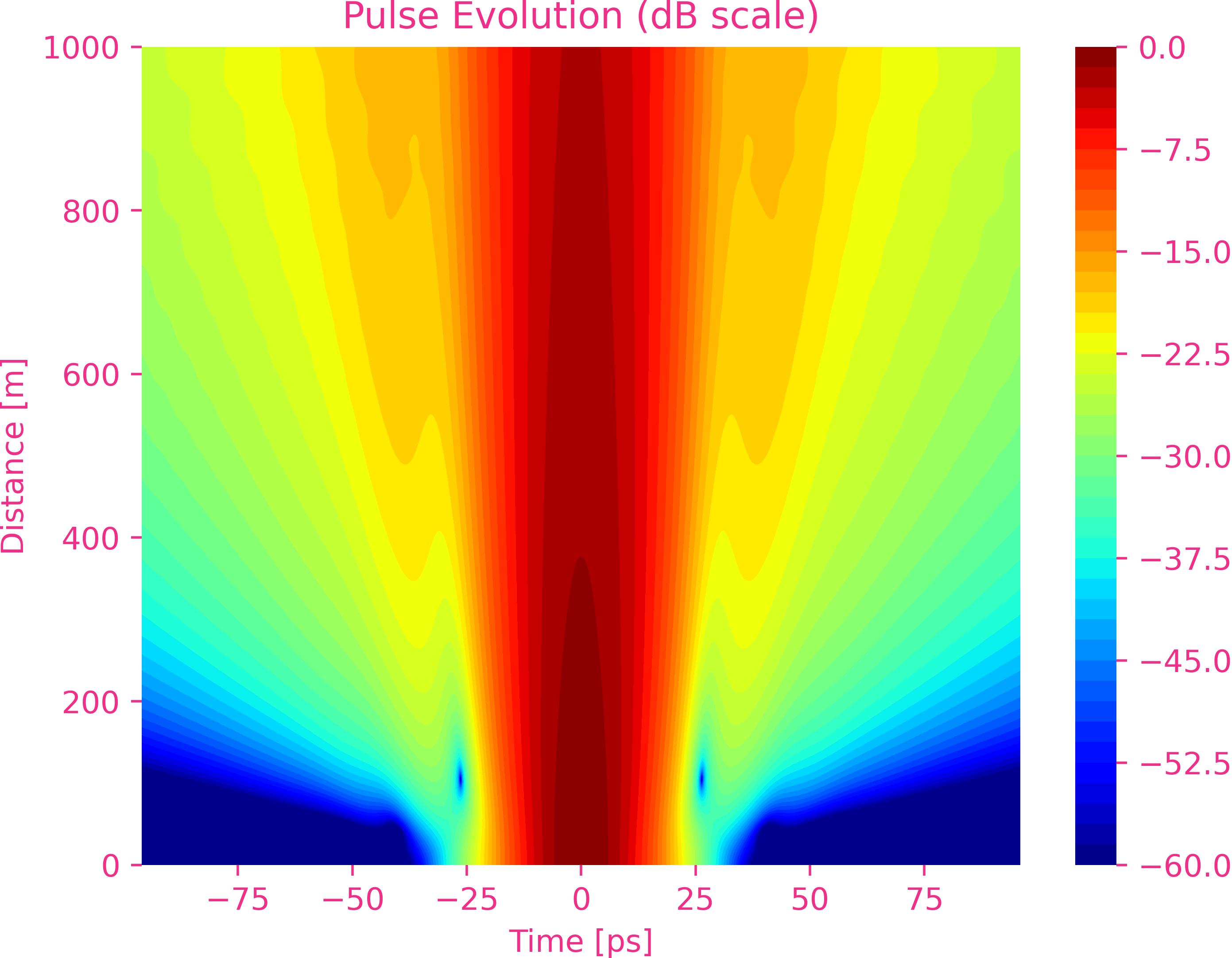
Fifth-order dispersion
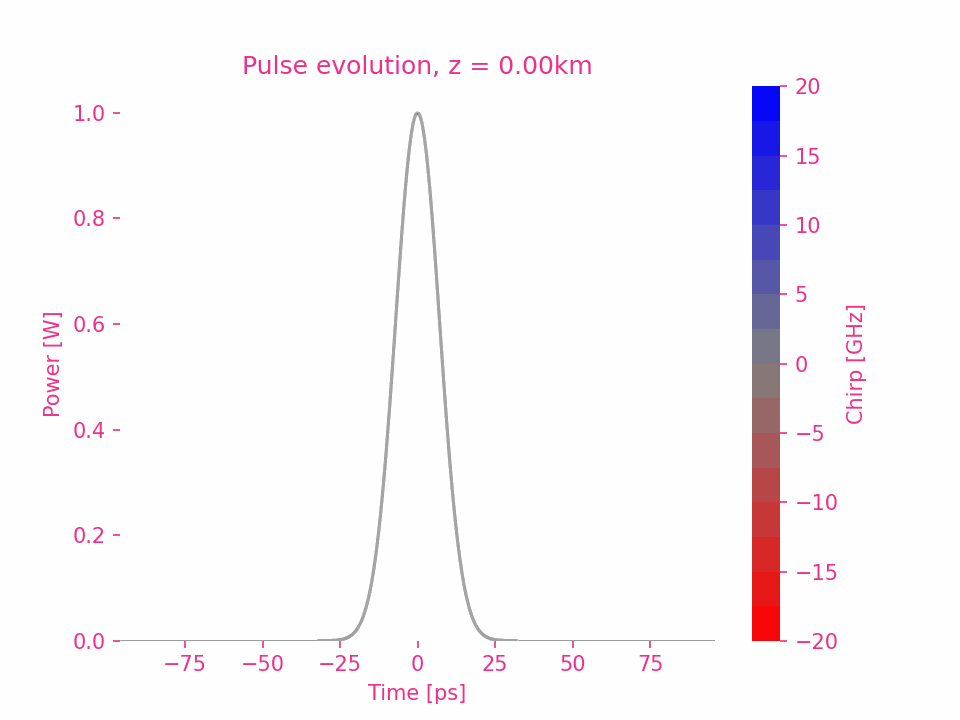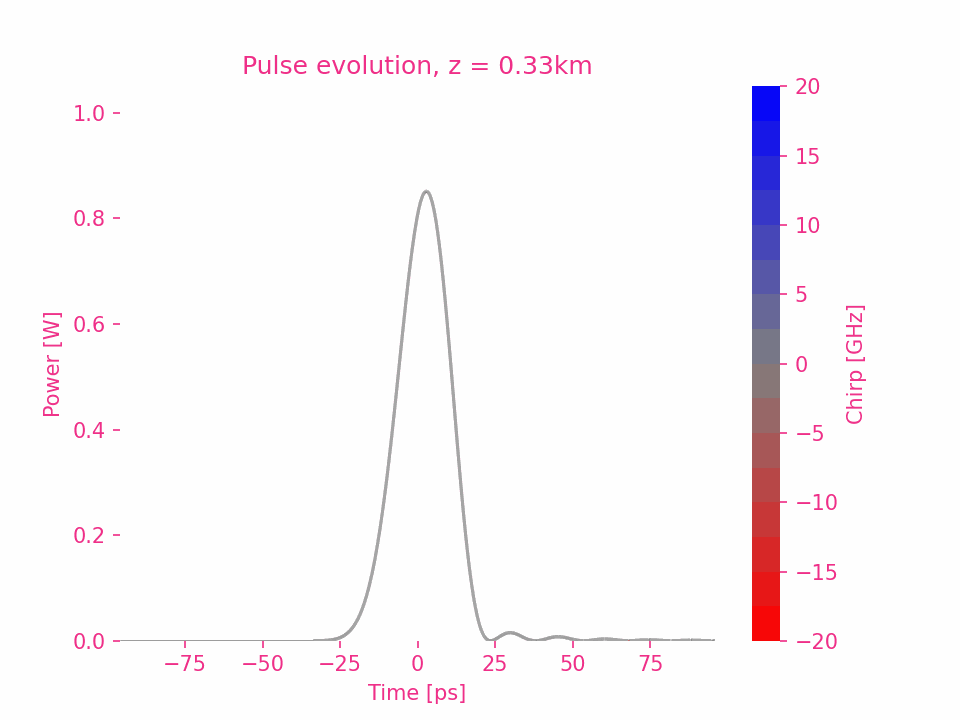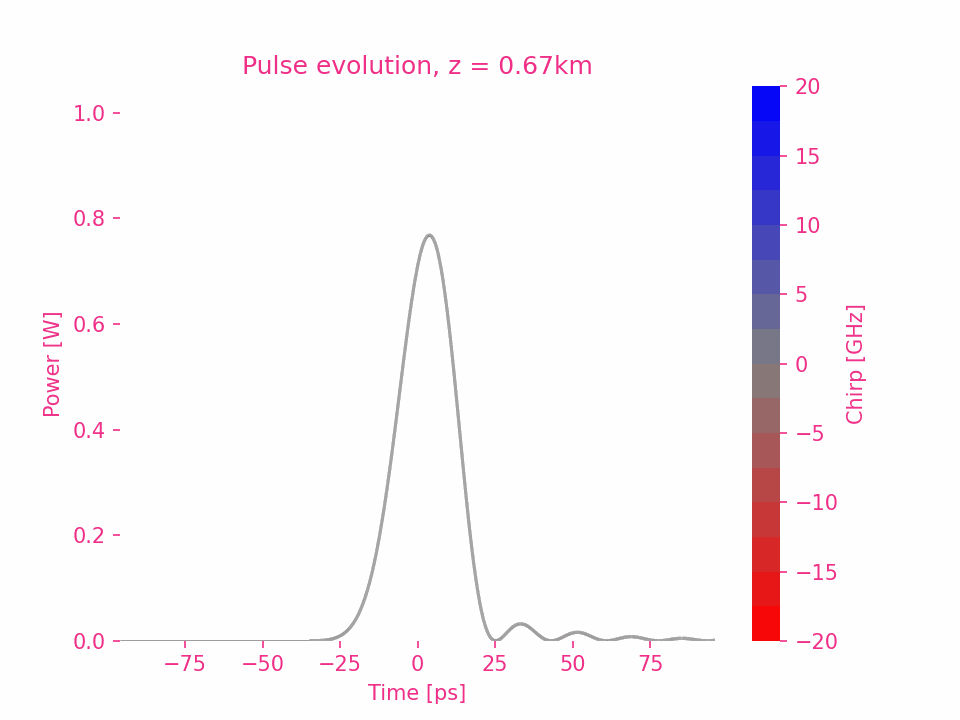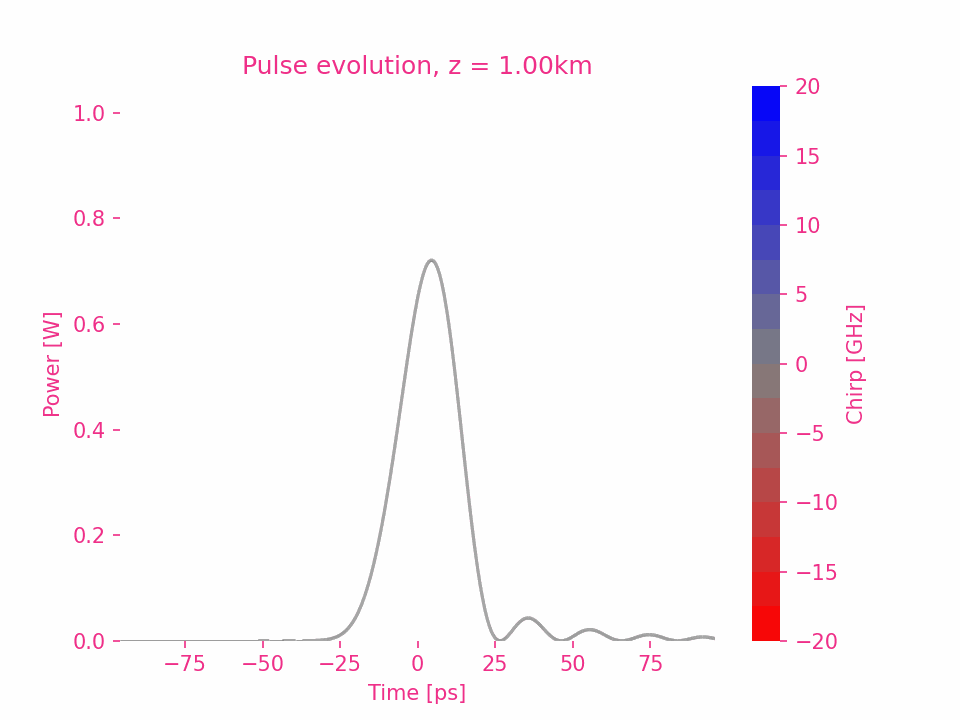
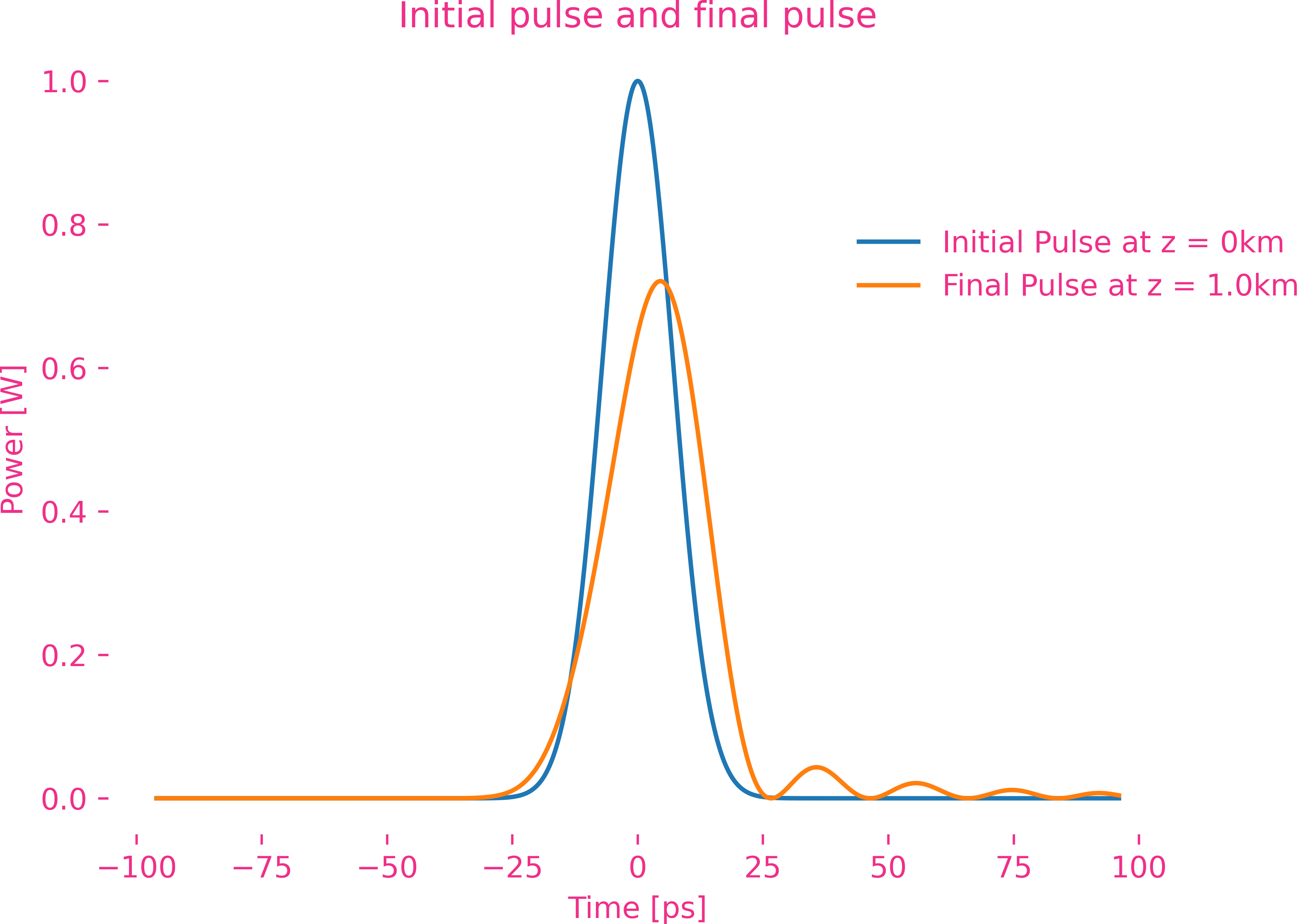
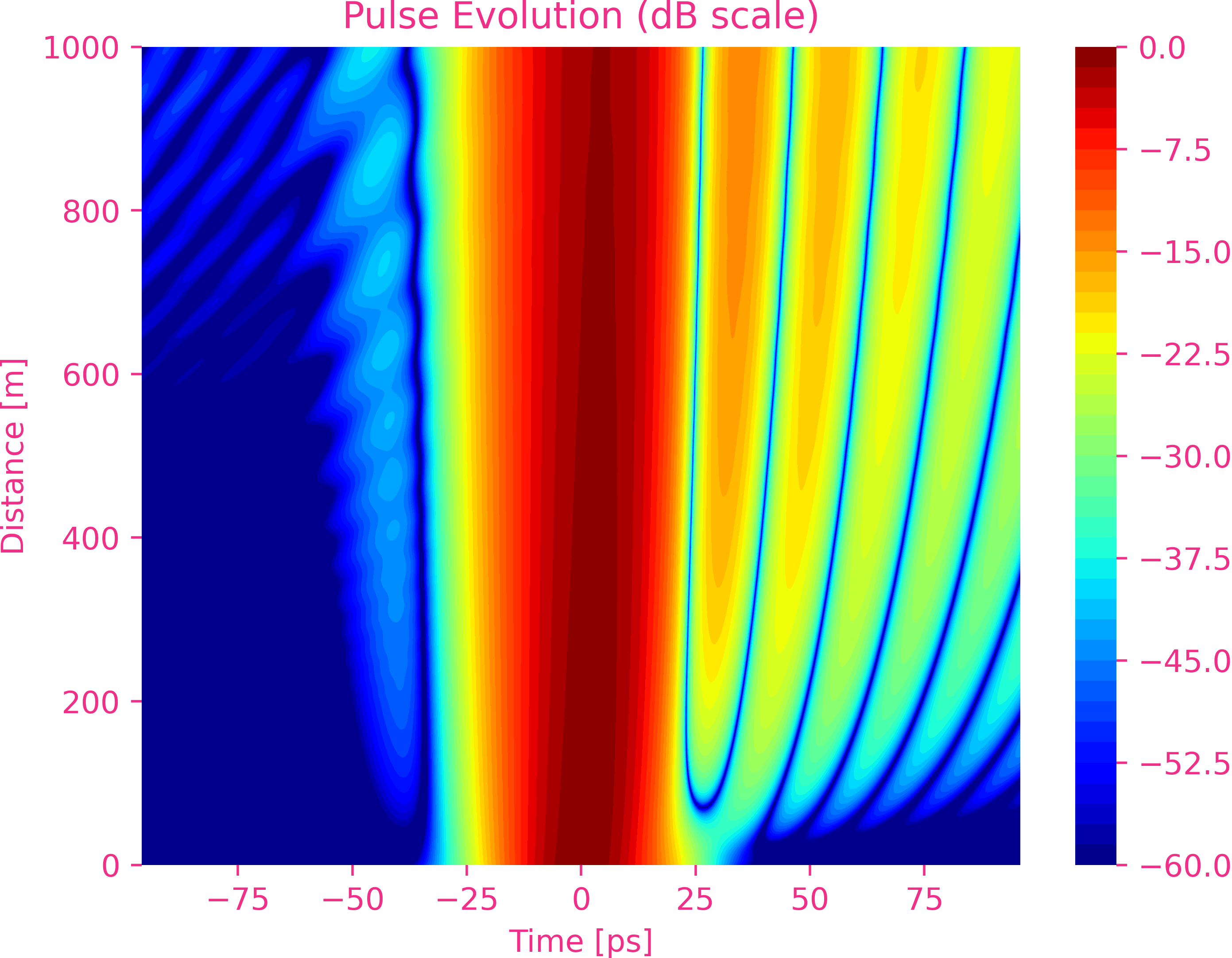
Sixth-order dispersion
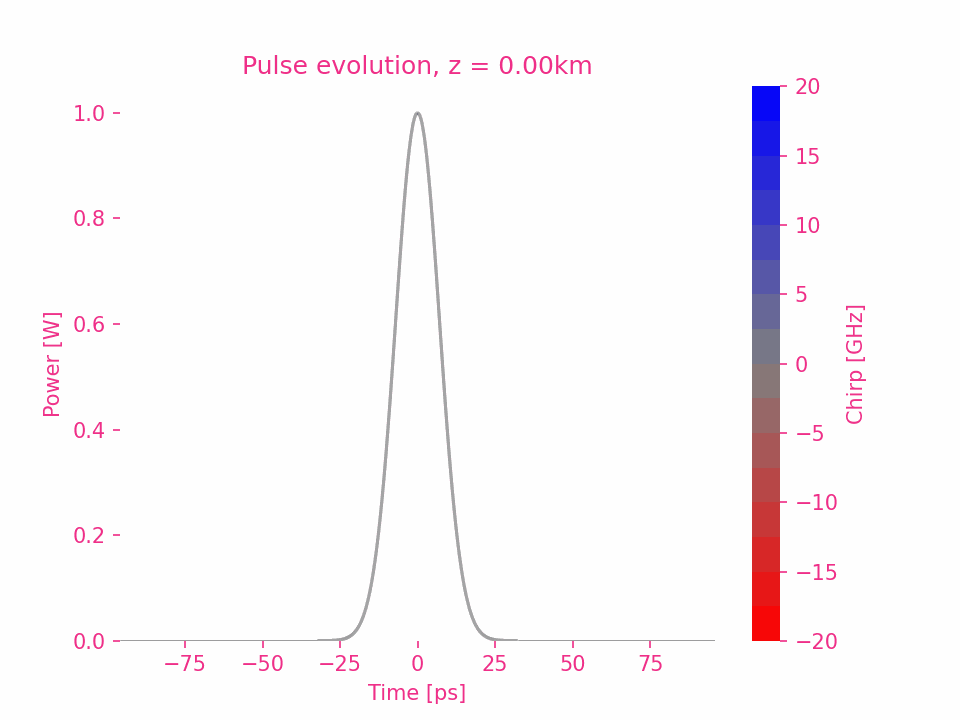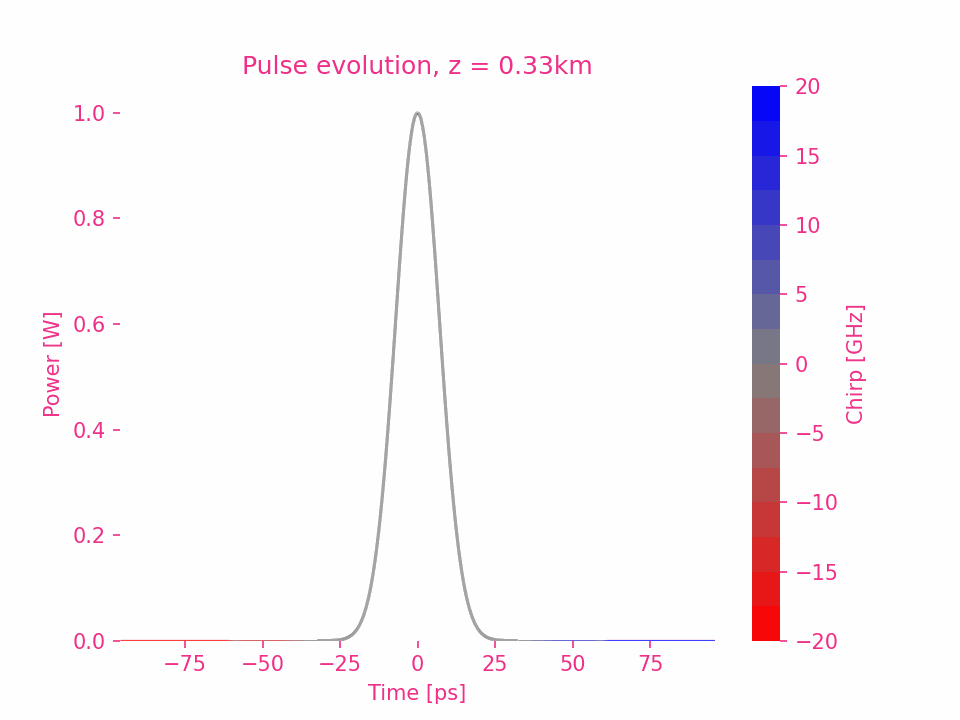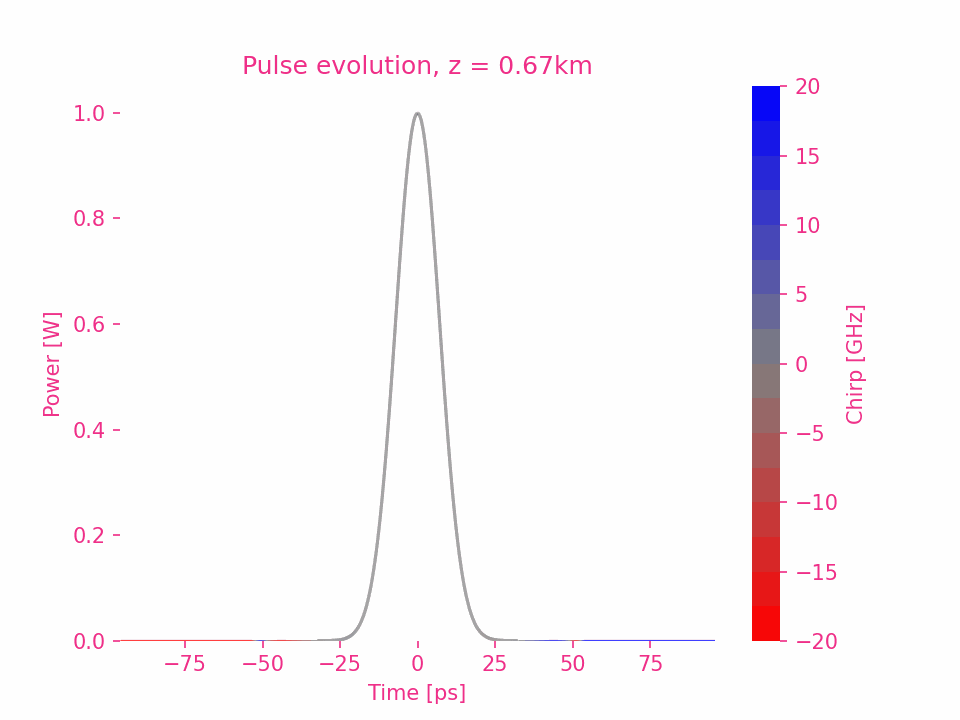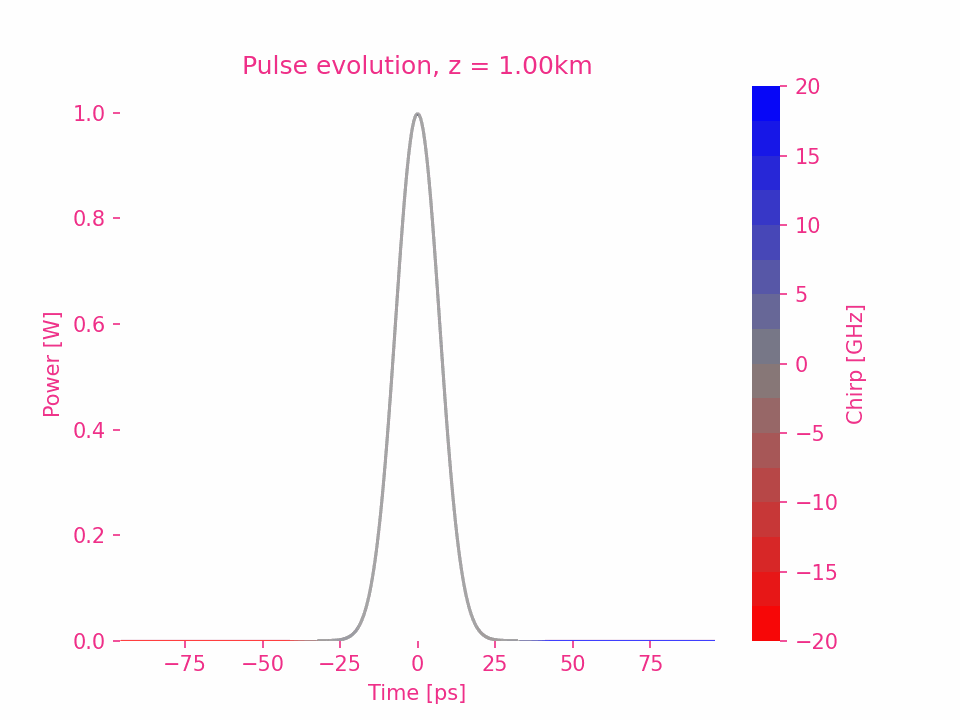
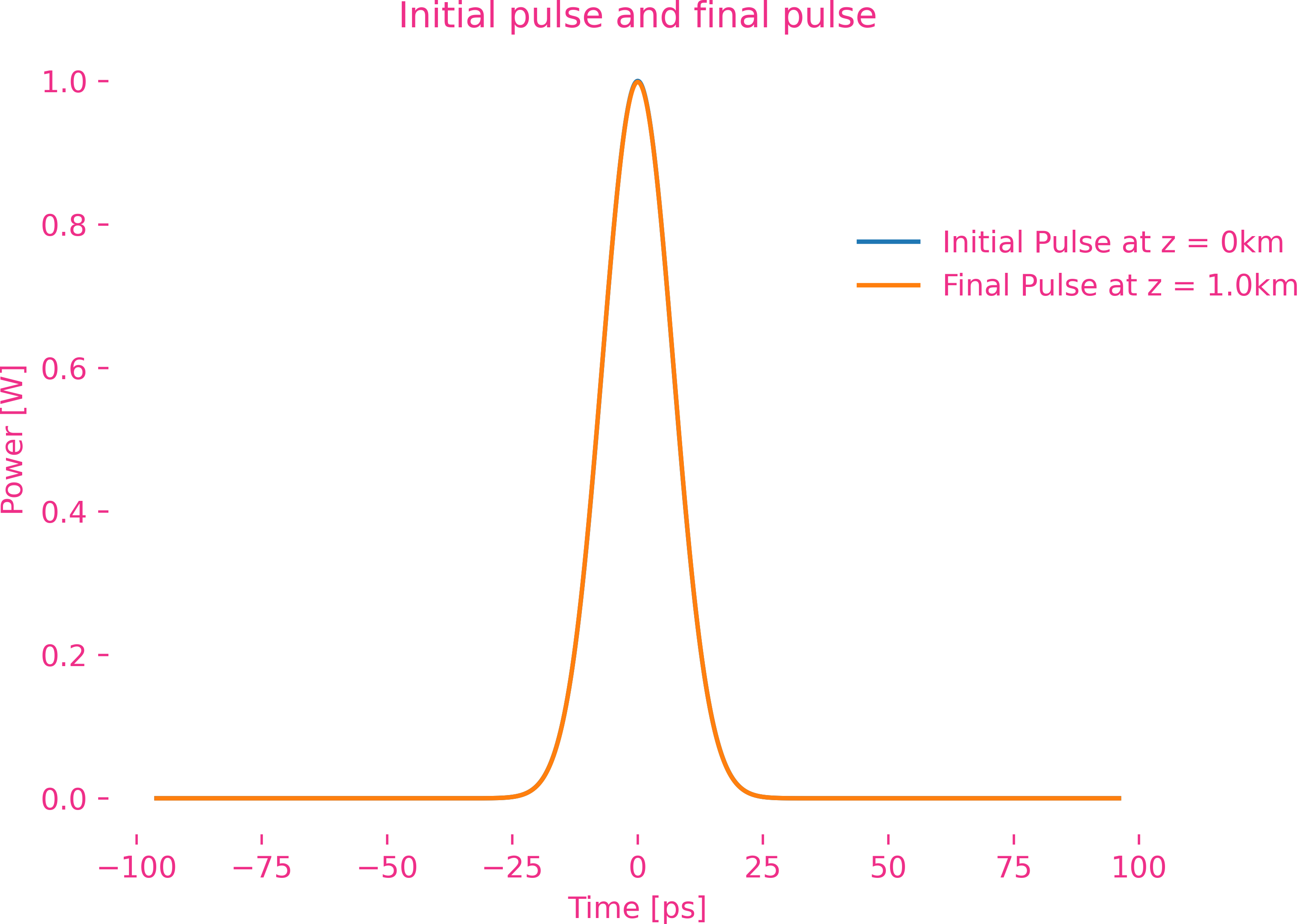
To be continue…
啁啾高斯脉冲
双曲正割脉冲
超高斯脉冲
Understanding High Order Dispersion