Résoudre l'équation de Schrödinger non linéaire en Python
Cet article contient plusieurs images .GIF, ce qui peut ralentir la vitesse de chargement de la page web.
Lorsqu’on considère l’influence de la dispersion d’ordre supérieur sur la transmission d’impulsions, l’atténuation $\alpha$ et le paramètre non linéaire $\gamma$ dans l’équation de transmission d’impulsions sont généralement simplifiés à 0 pour plus de commodité. En même temps, l’intensité de l’impulsion $A$ est normalisée en $U$.
L’impulsion normalisée satisfait dans le domaine temporel :
$$
\mathrm{i}\frac{\partial U}{\partial z}=\frac{\beta_2}{2}\frac{\partial^2U}{\partial T^2}+\mathrm{i}\frac{\beta_3}{6}\frac{\partial^3U}{\partial T^3}+…
$$
En domaine fréquentiel, cela devient:
$$
\frac{\partial U}{\partial z}=\mathrm{i}[\frac{\beta_2}{2}(\omega-\omega_0)^2+\frac{\beta_3}{6}(\omega-\omega_0)^3+…]\widetilde U
$$
Il montre que lorsqu’une impulsion optique est transmise à travers une fibre optique, chaque composante spectrale dans son enveloppe subit un déphasage dépendant de la fréquence.
La solution générale de l’équation dans le domaine de la fréquence est:
$$
\widetilde{U}(z, \omega)=\widetilde{U}(0, \omega)\mathrm{e}^{\mathrm{i}\frac{\beta_2}{2}(\omega-\omega_0)^2z+\mathrm{i}\frac{\beta_3}{6}(\omega-\omega_0)^3z+…}
$$
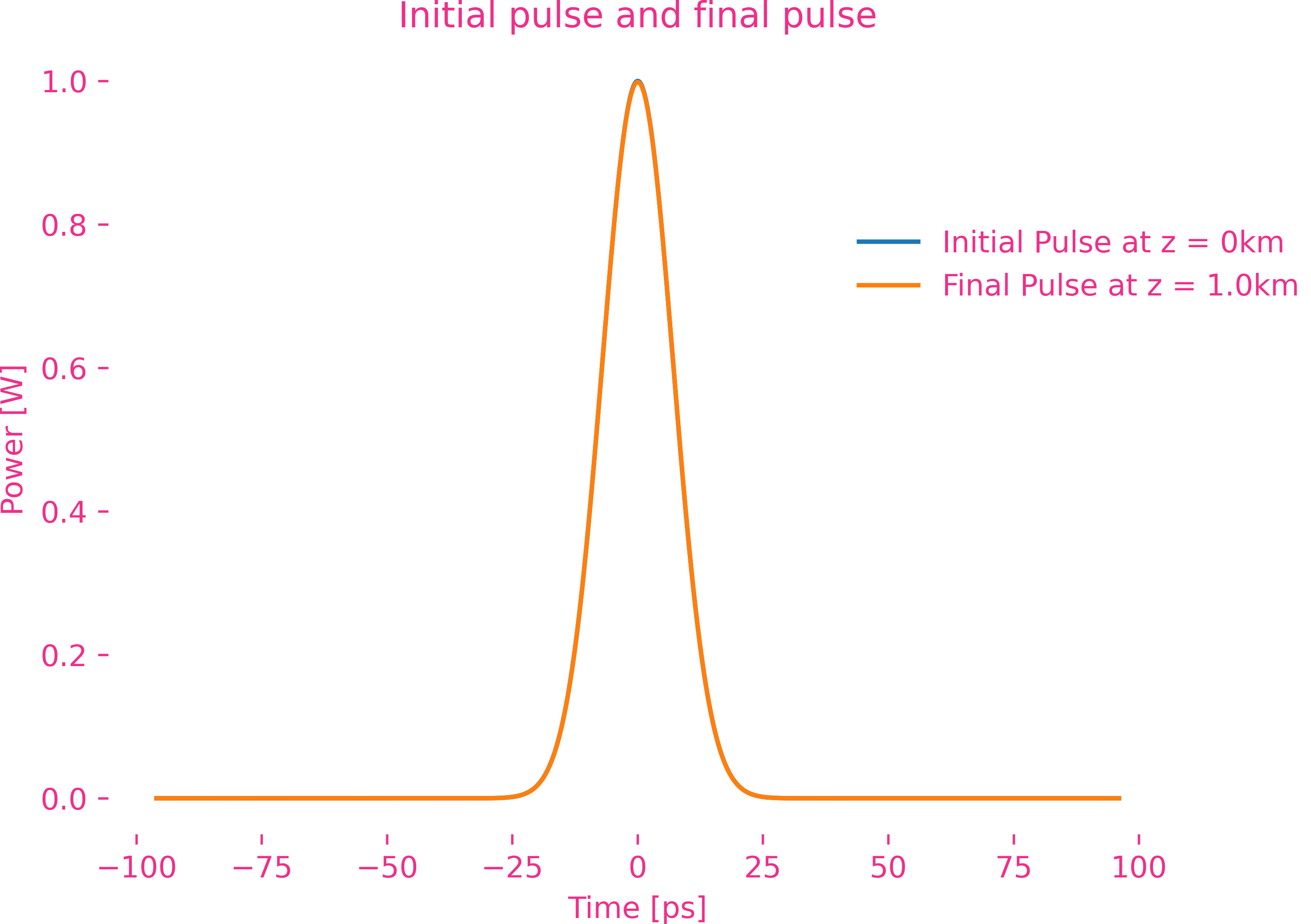
Ensuite, en prenant l’impulsion gaussienne comme exemple, nous analyserons séparément l’impact de chaque ordre de dispersion sur la transmission d’impulsion.
Consultez le code source dans mon référentiel GitHub.
Dispersion de vitesse de groupe d’une impulsion gaussienne
En prenant $\beta_2>0$ comme exemple, le déphasage de chaque composante de fréquence dans l’impulsion est égal au carré de la différence entre la fréquence de la composante et la fréquence centrale.
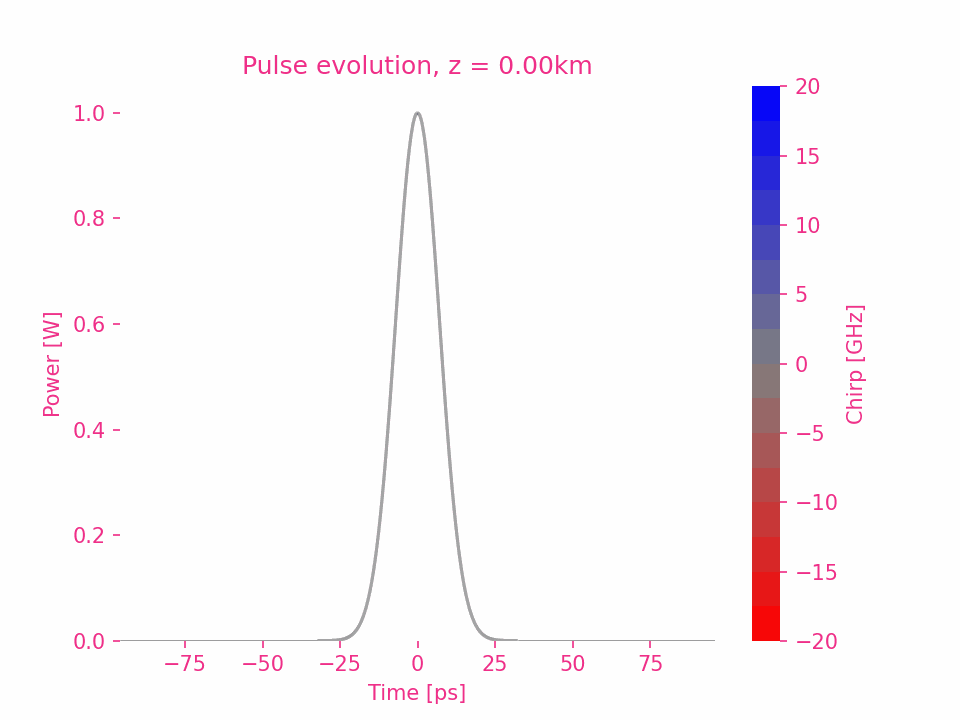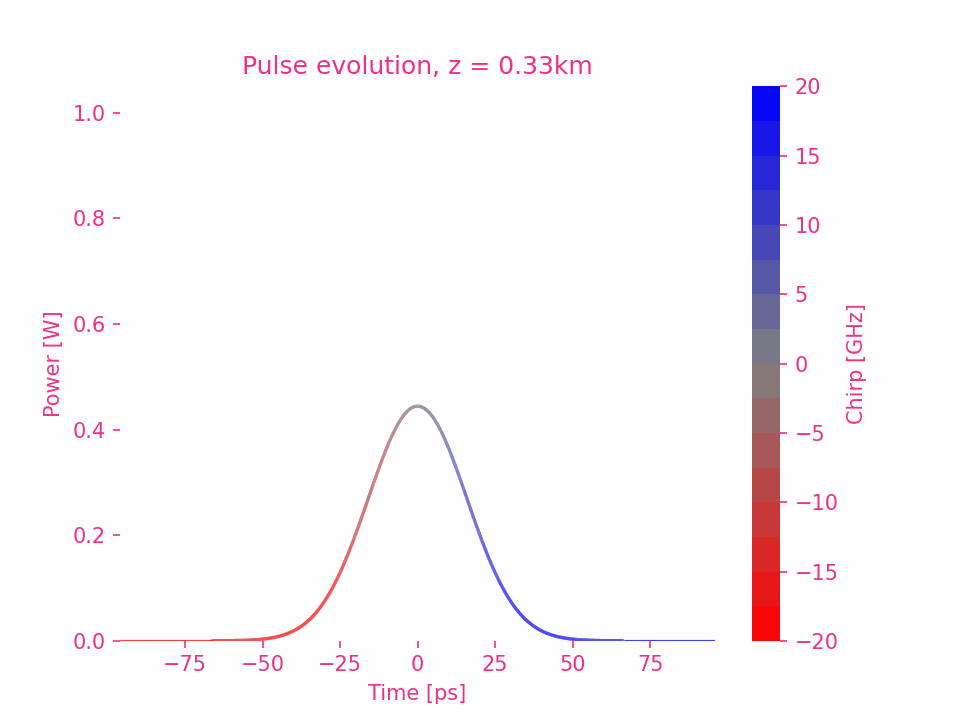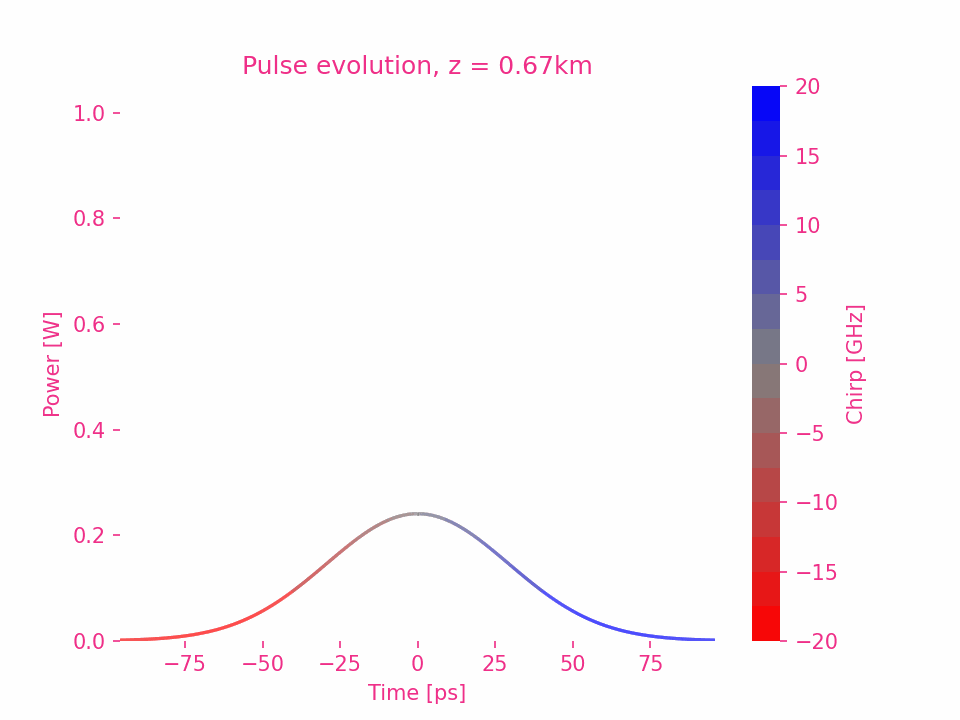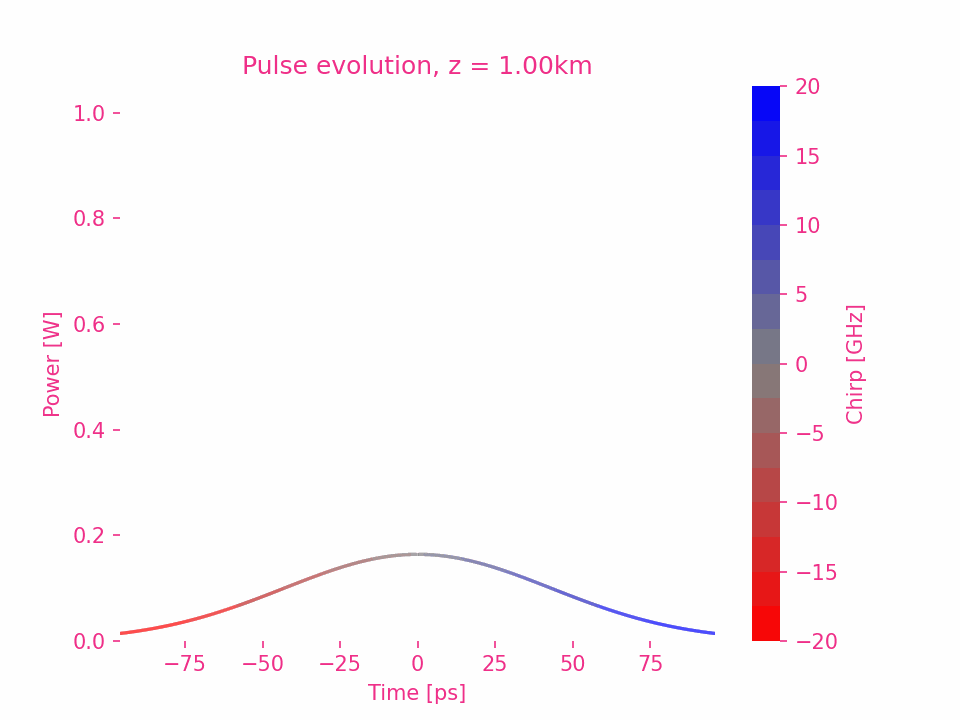
Dispersion du troisième ordre d’une impulsion gaussienne
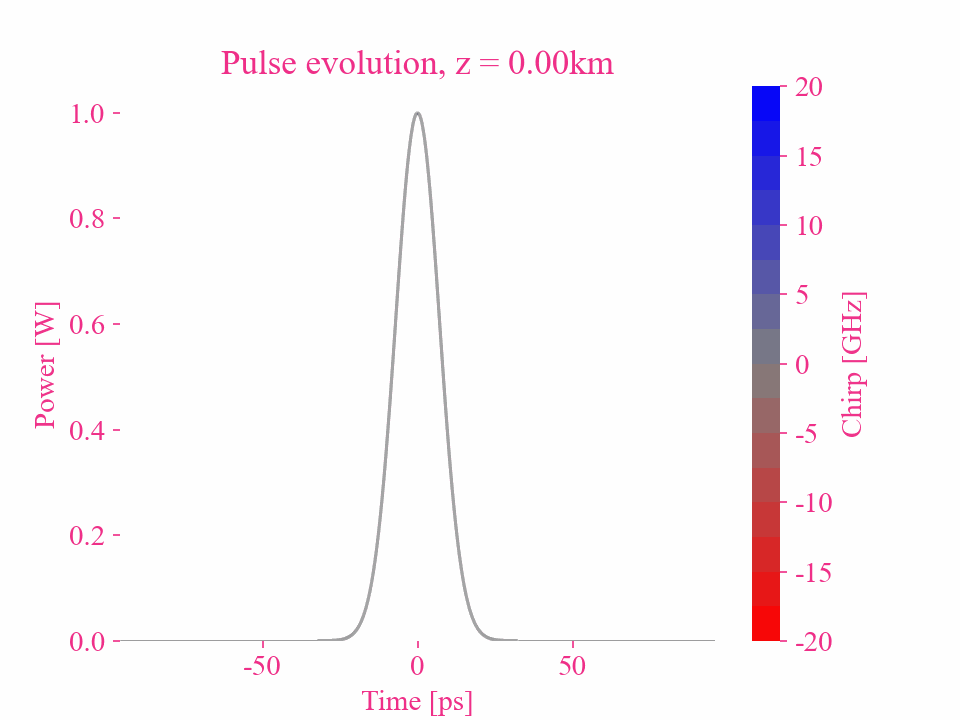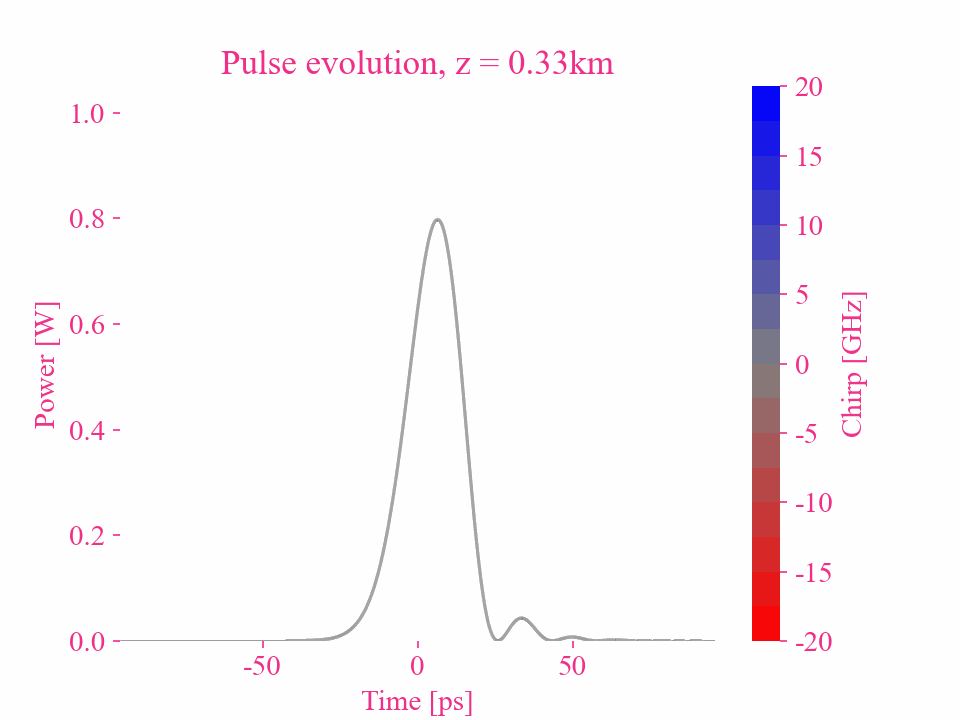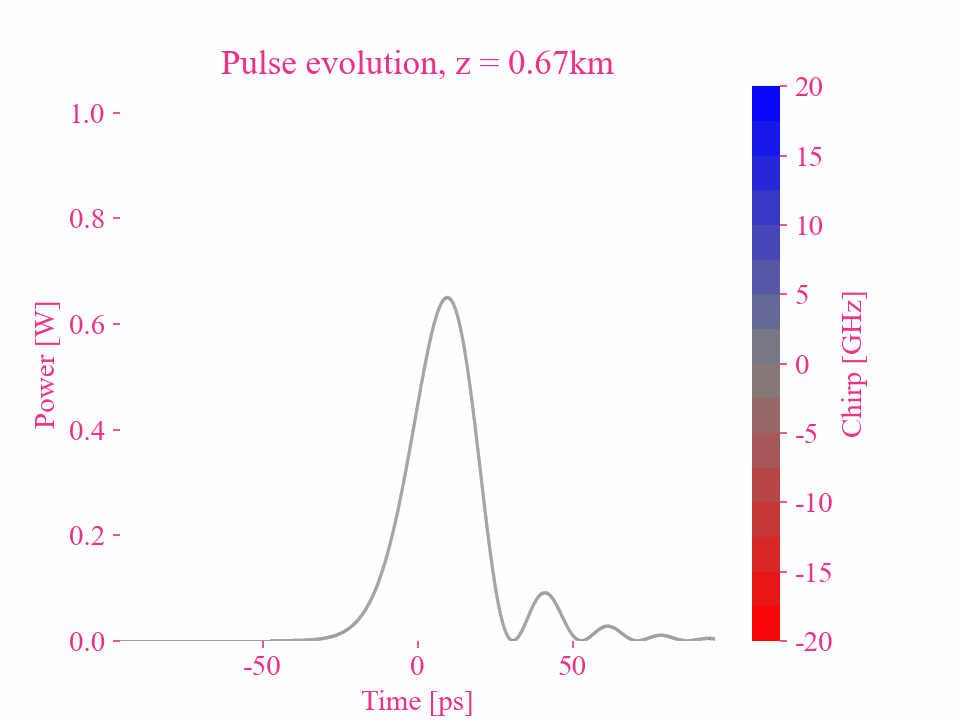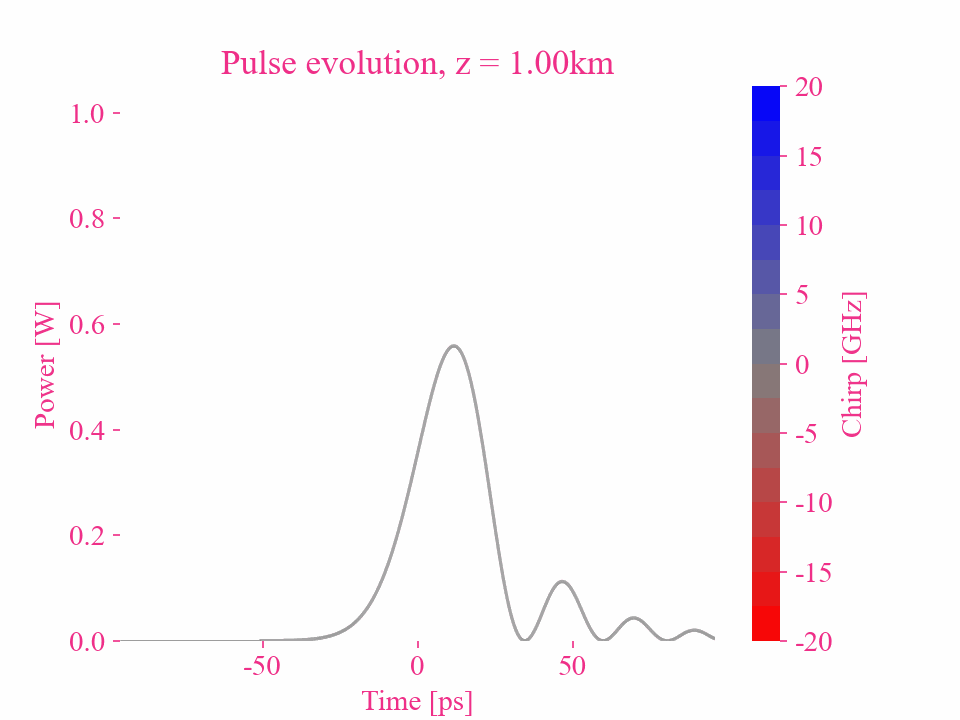
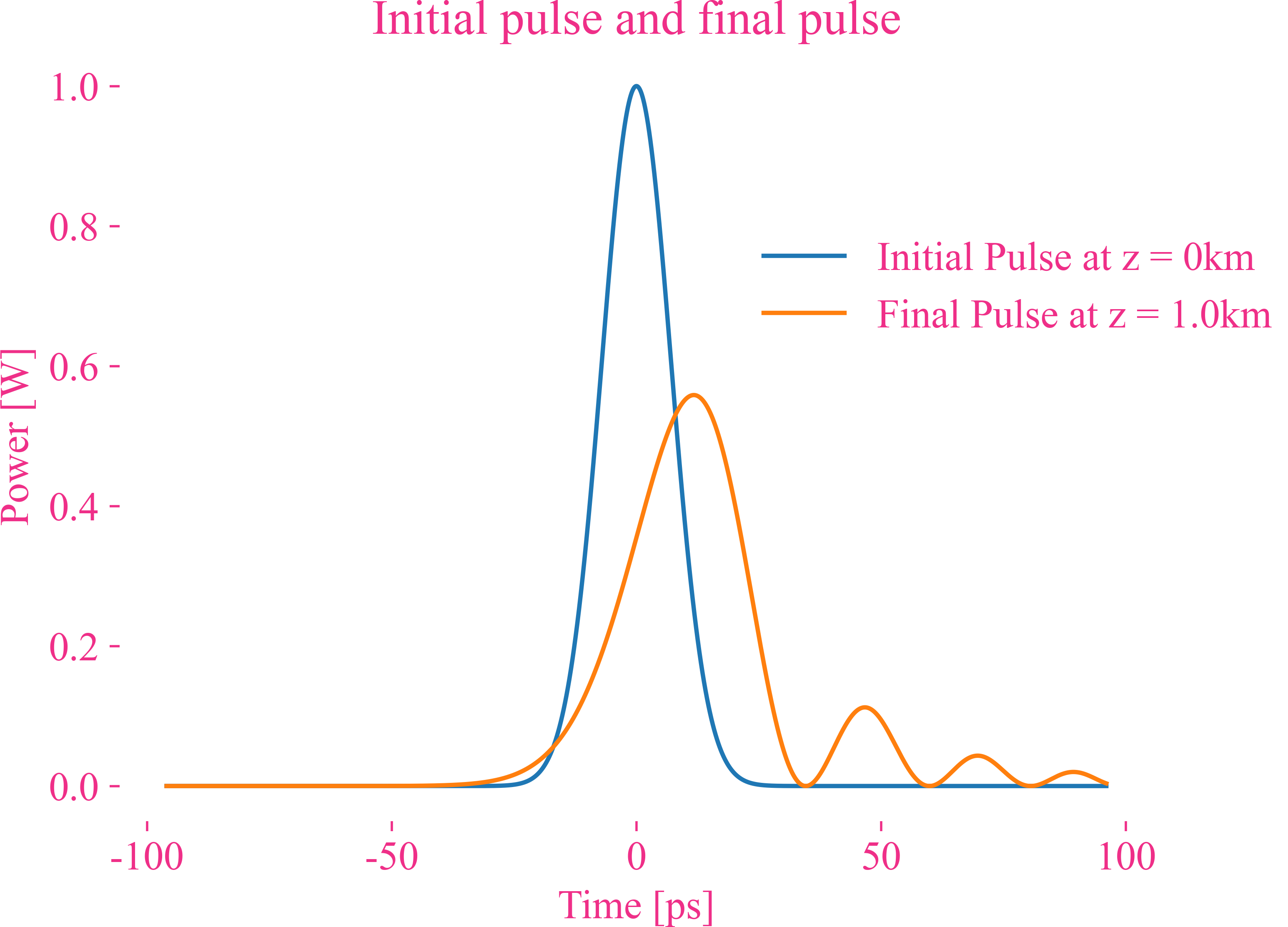
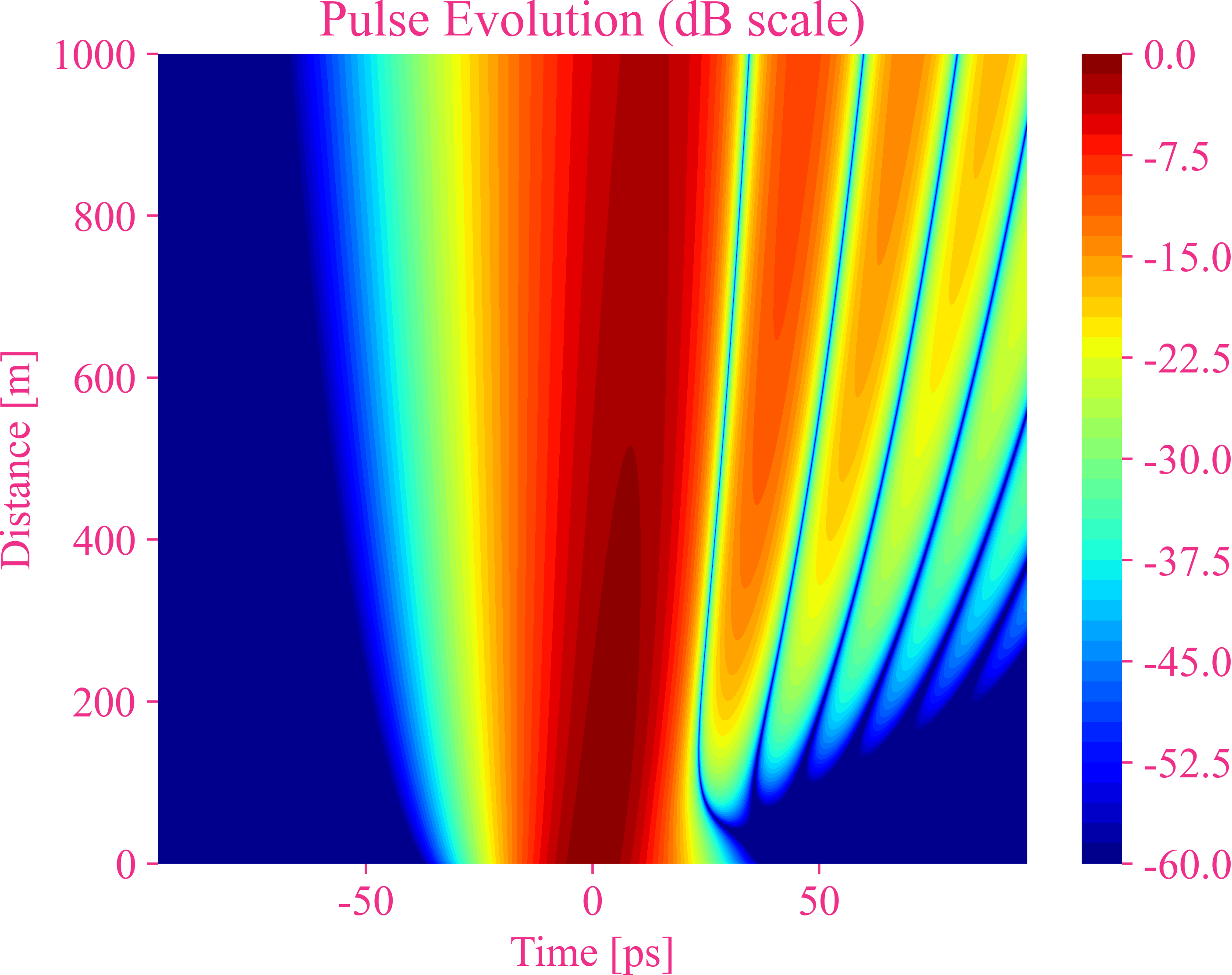
Dispersion d’ordre supérieur d’une impulsion gaussienne
Dispersion du quatrième ordre
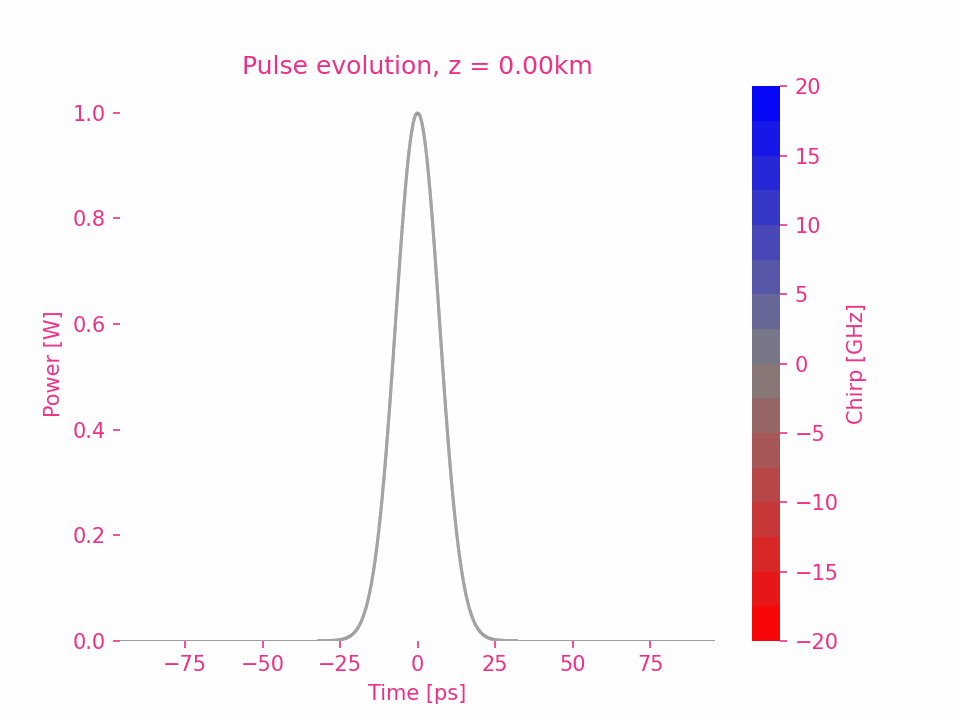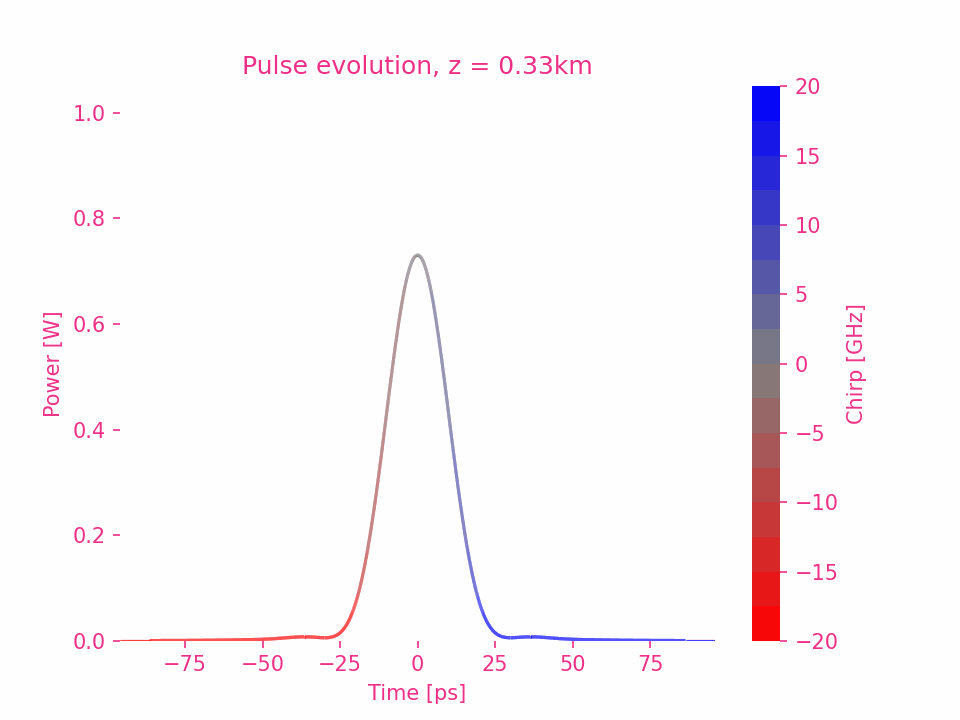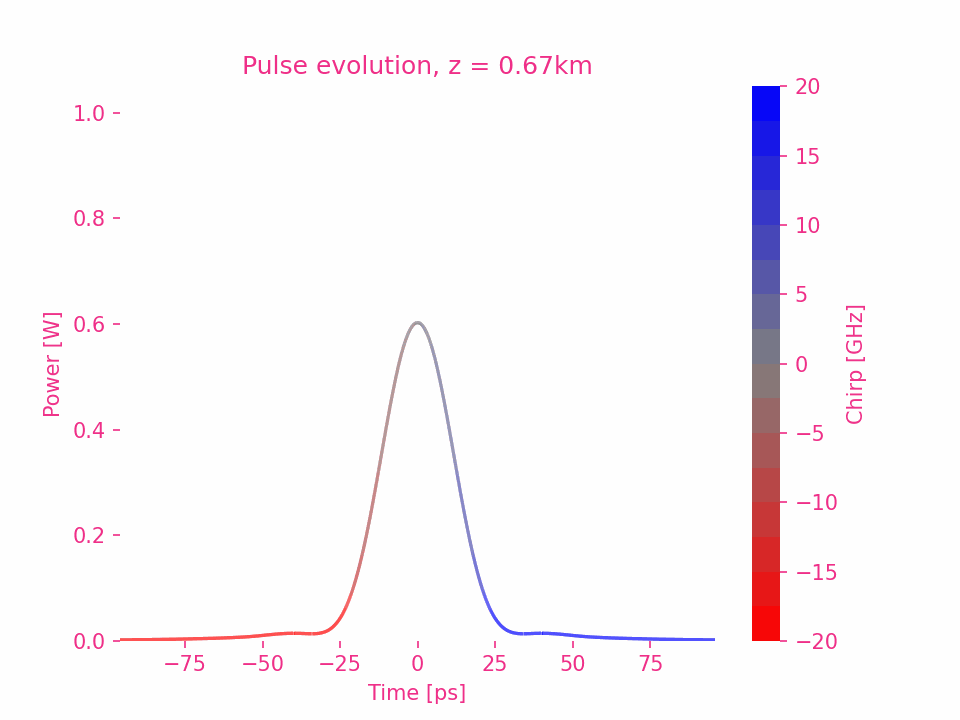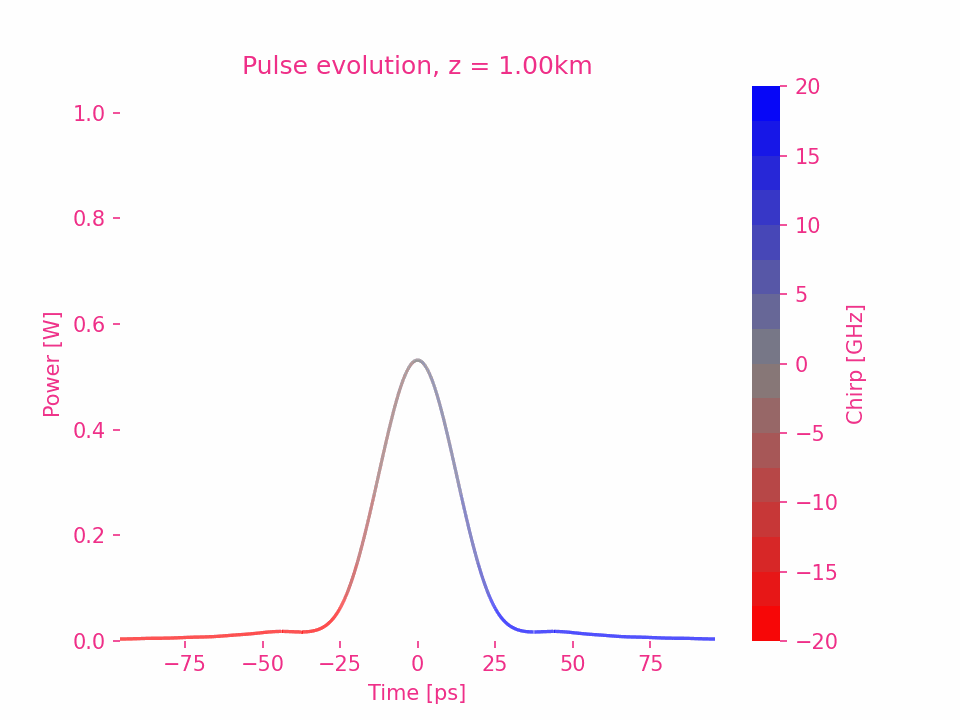
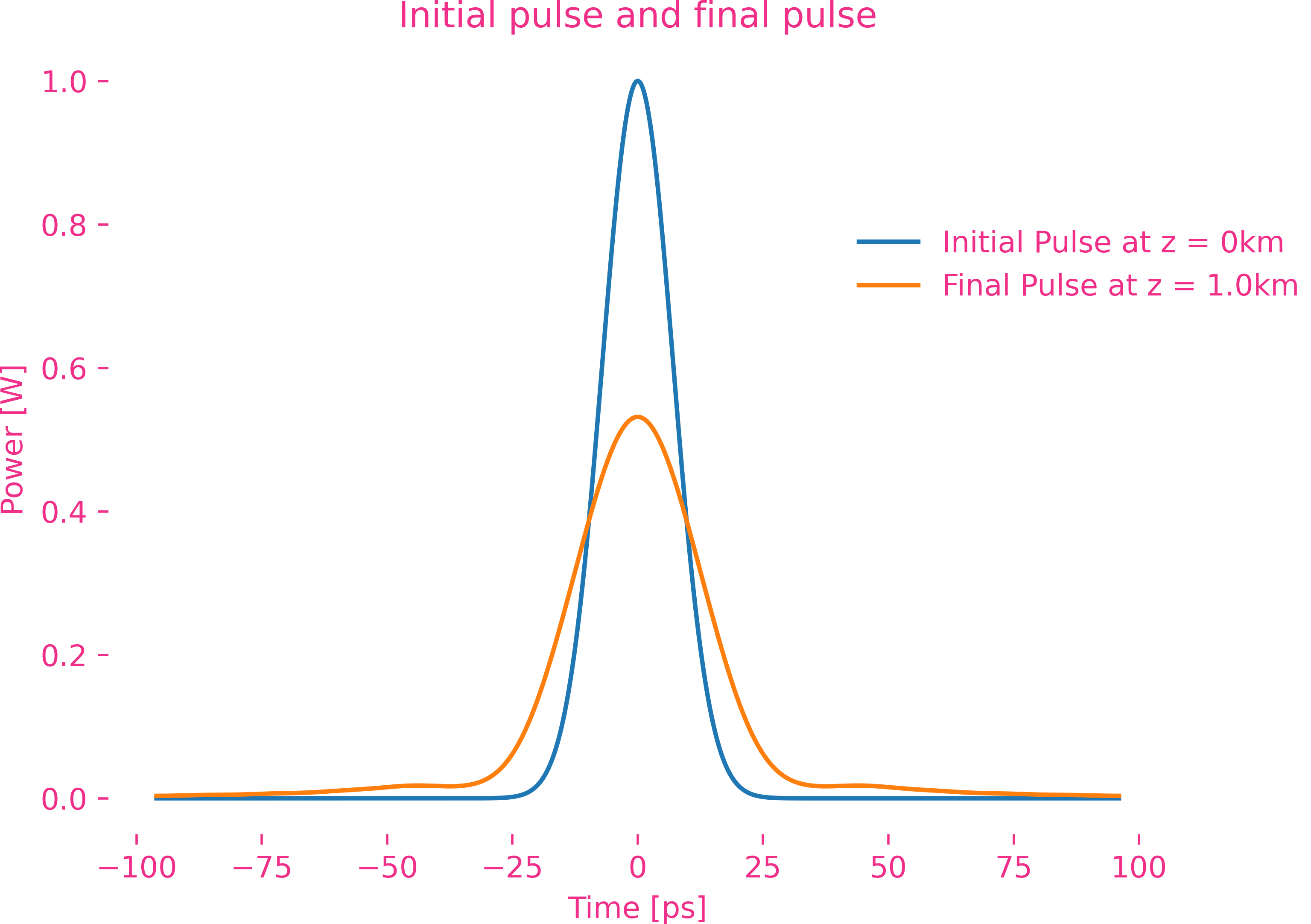
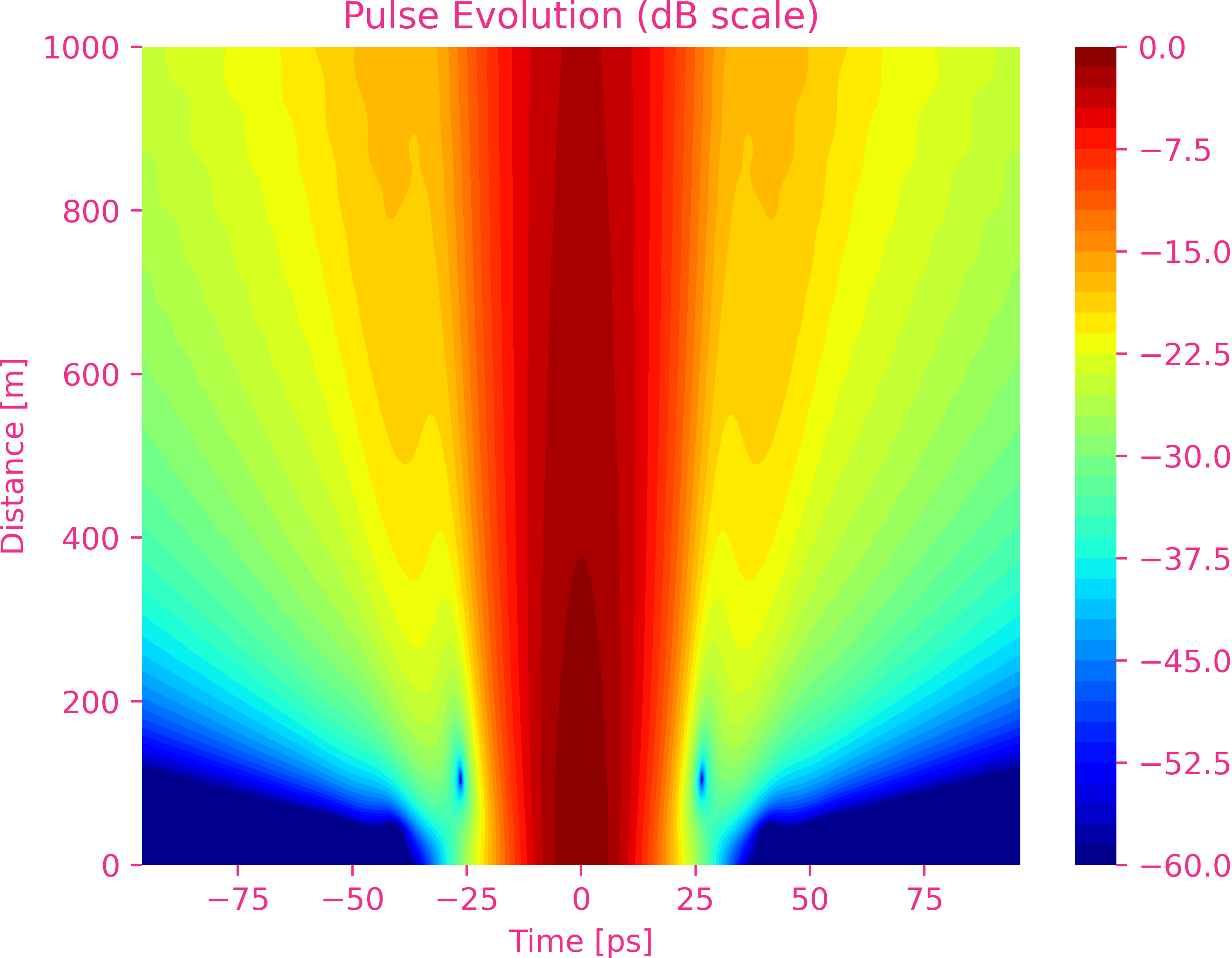
La dispersion d’ordre cinq
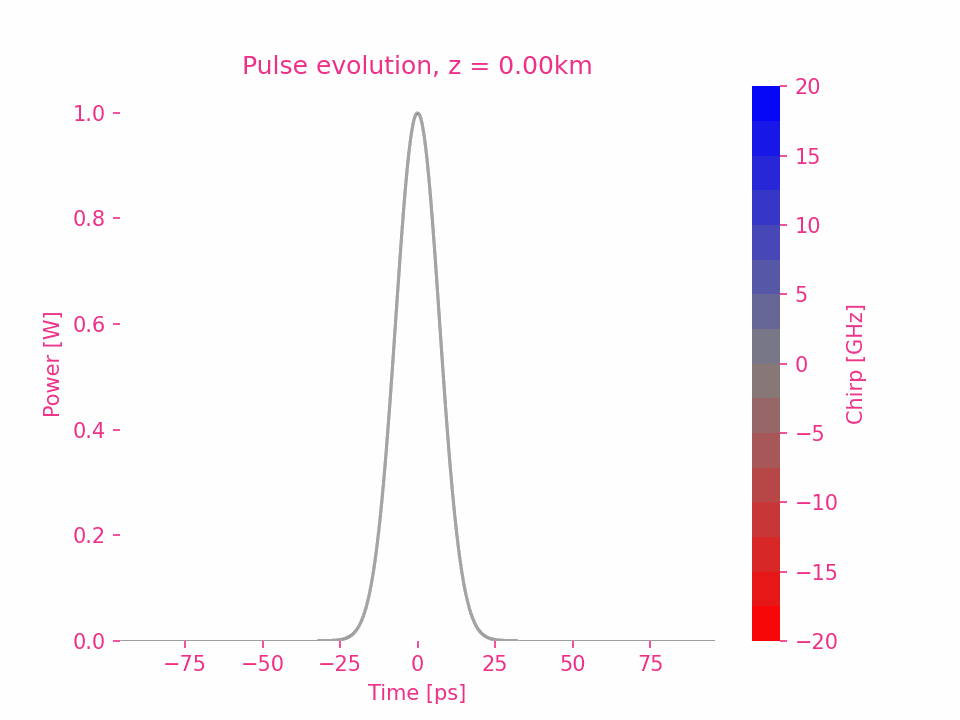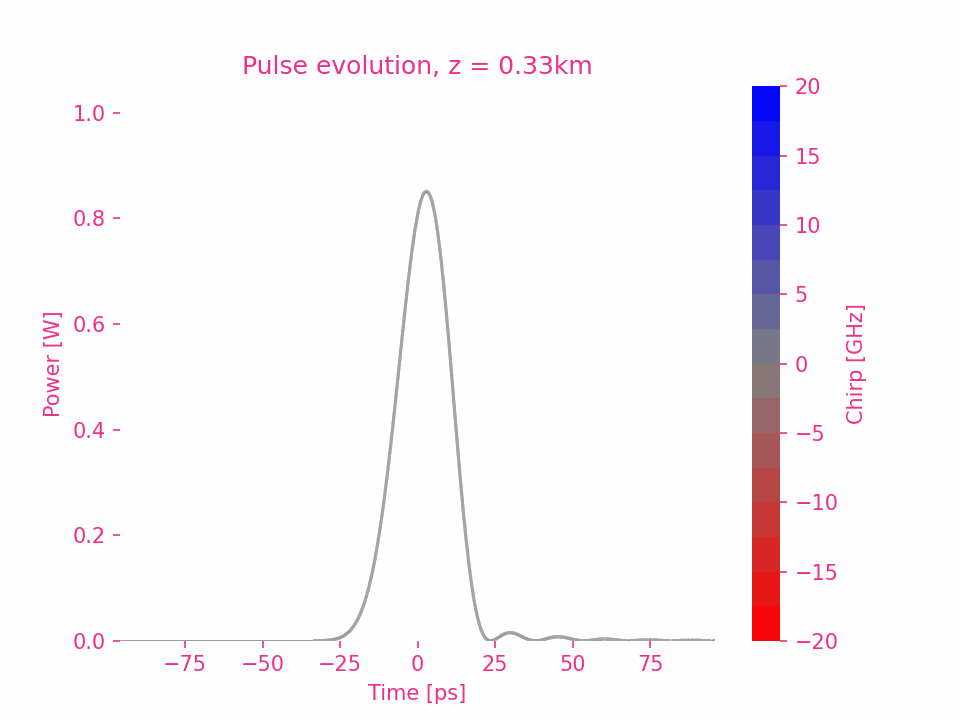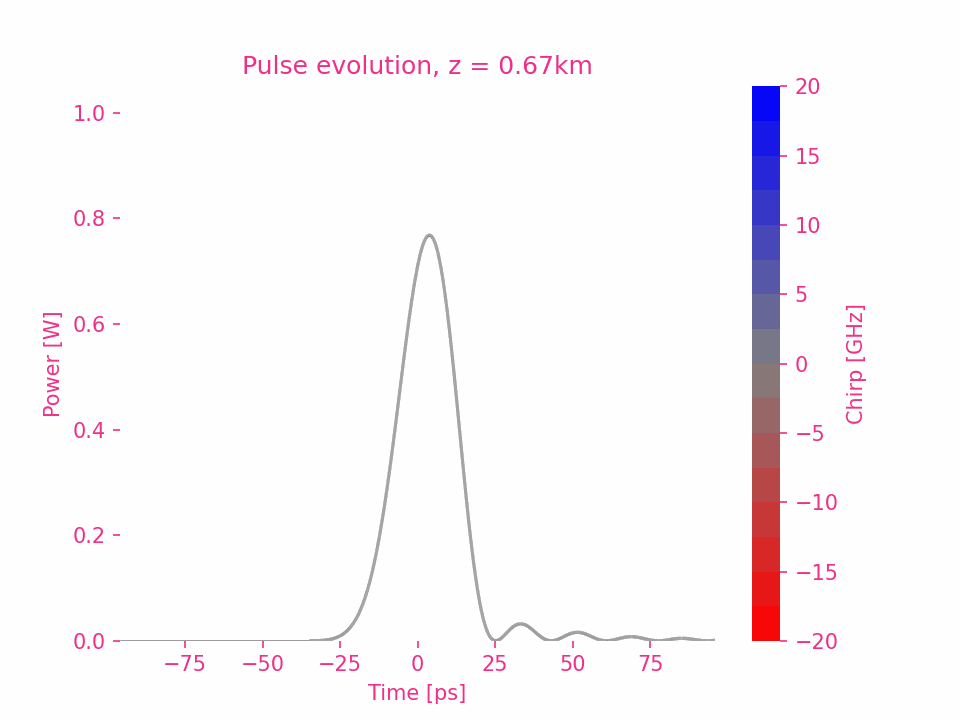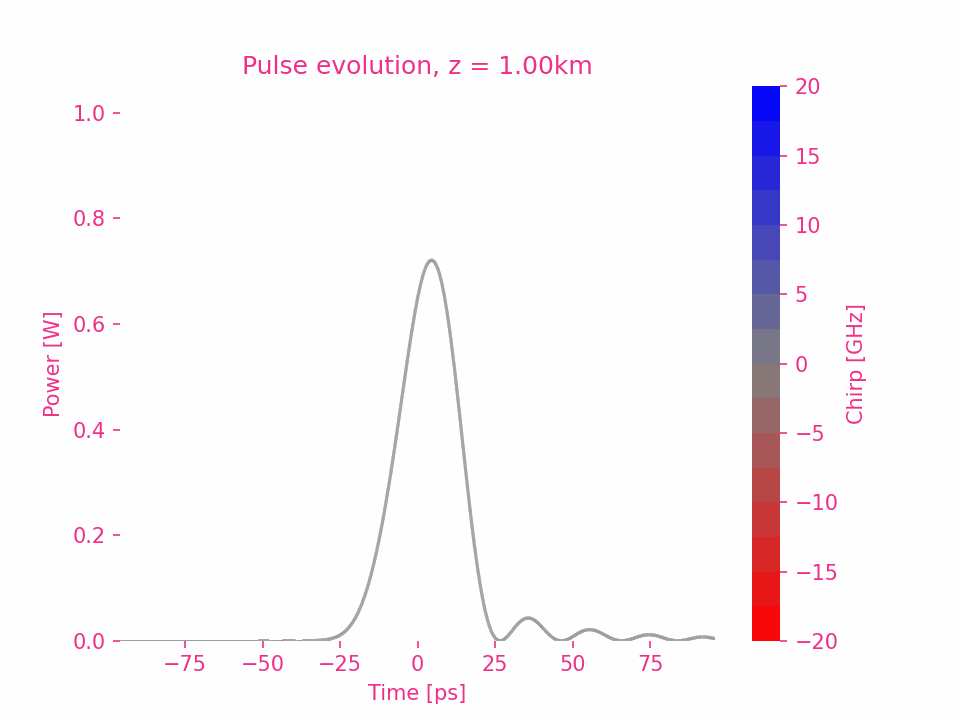
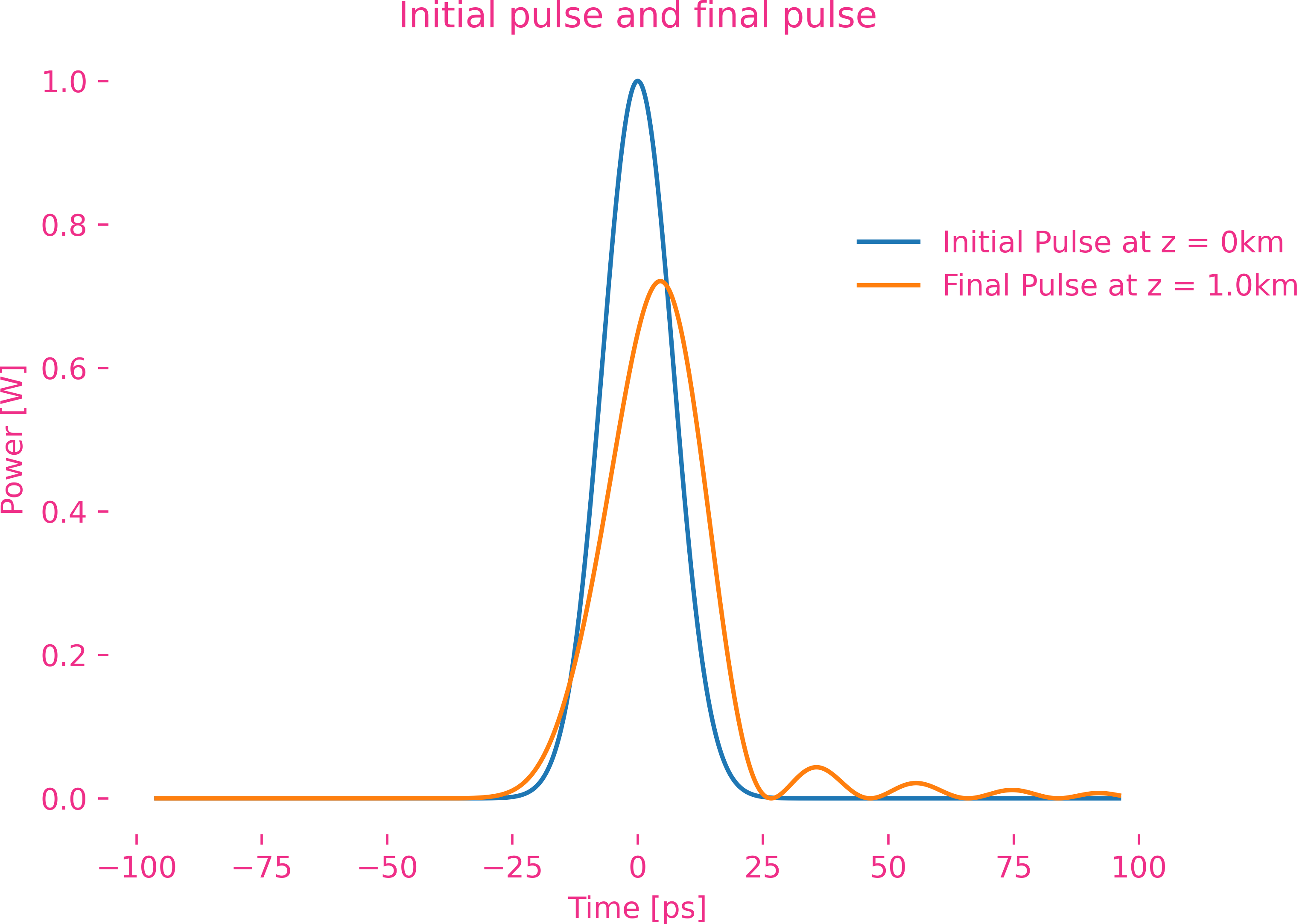
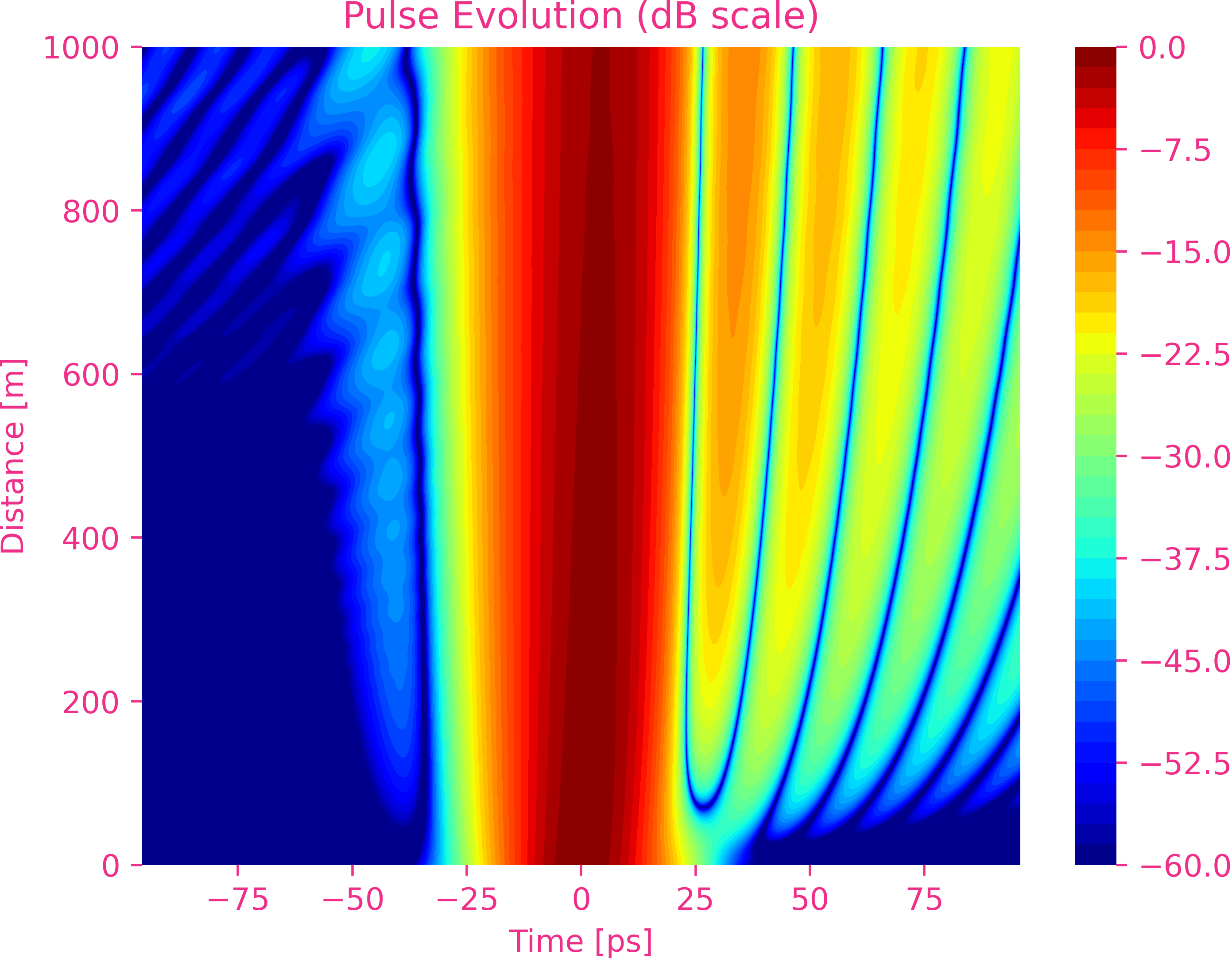
La dispersion d’ordre six
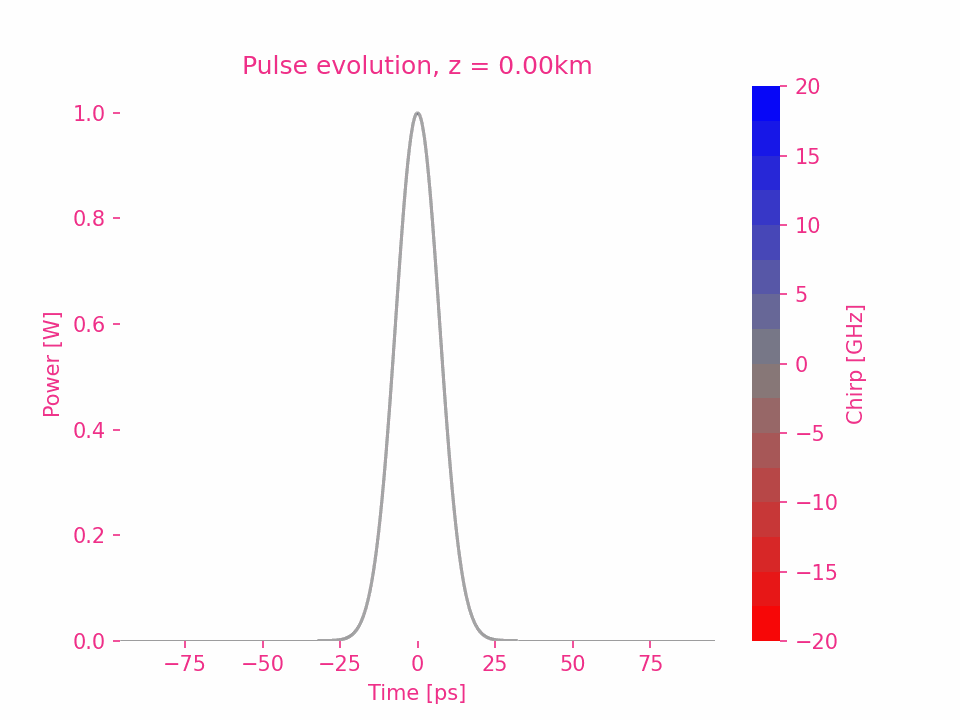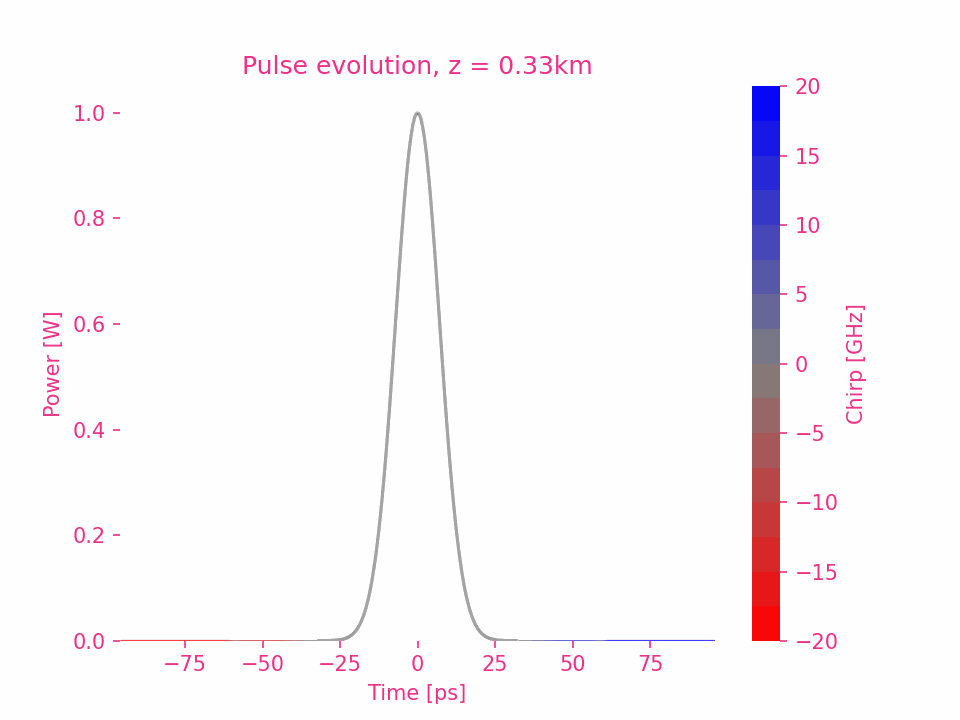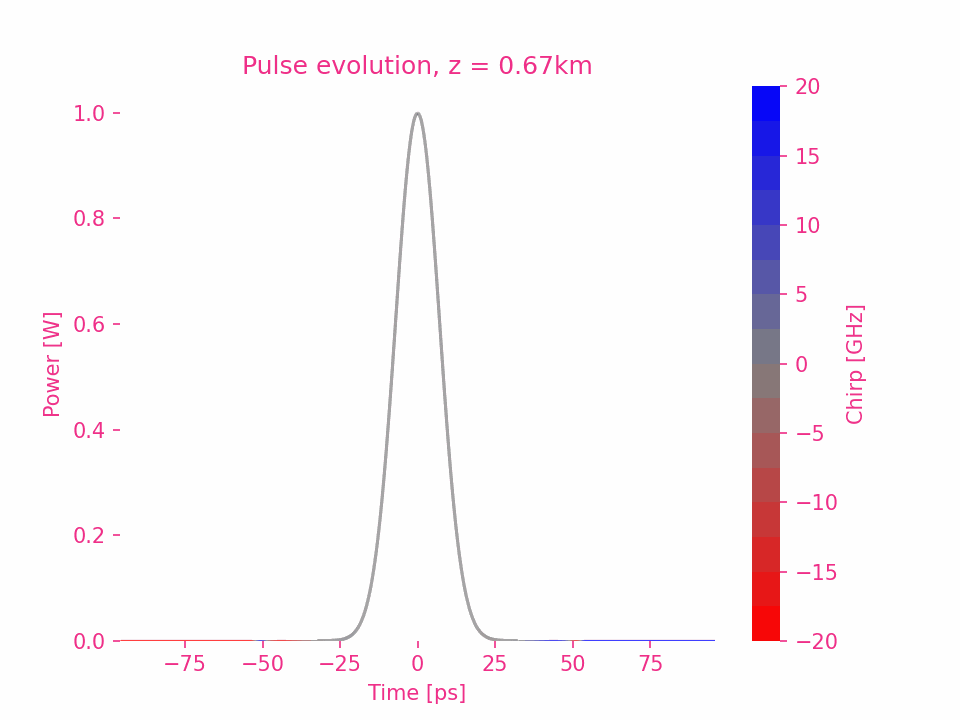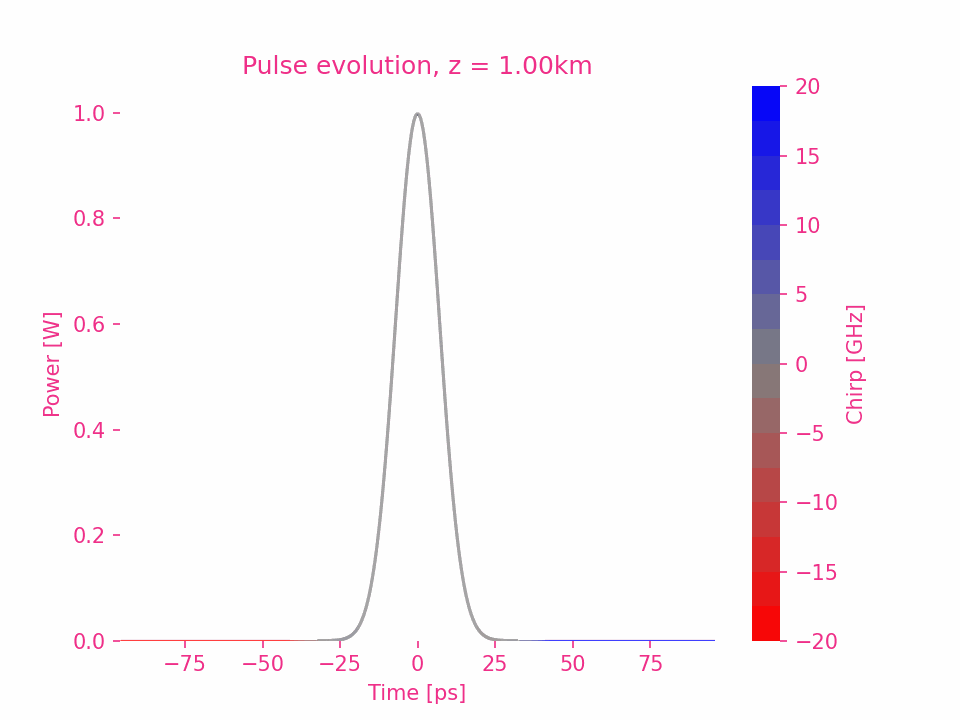
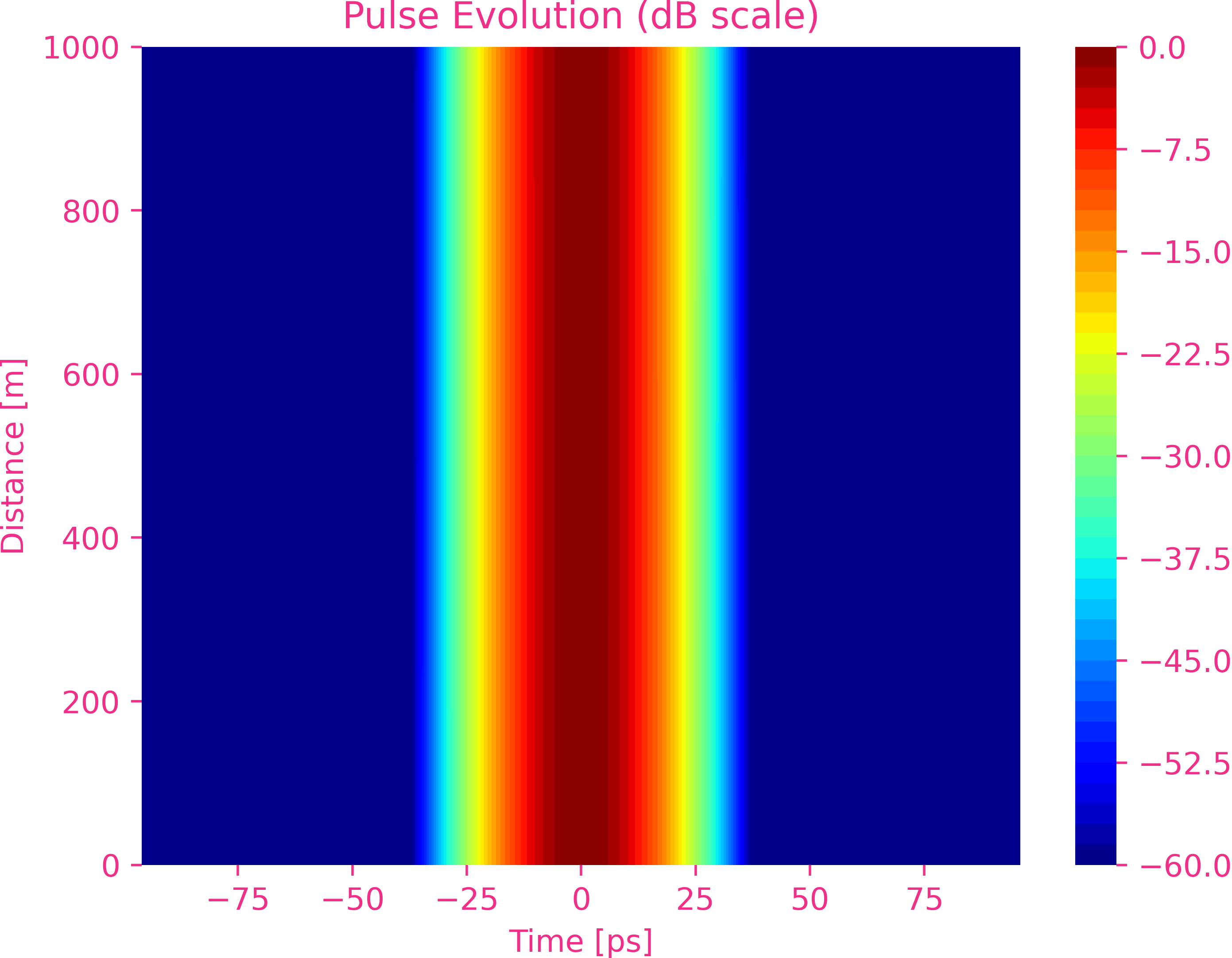
To be continue…
啁啾高斯脉冲
双曲正割脉冲
超高斯脉冲
Résoudre l'équation de Schrödinger non linéaire en Python