Solving Nonlinear Schrödinger Equation in Python

The Nonlinear Schrödinger Equation( $\alpha=0$ )：
$$
\frac{\partial A}{\partial z}=-\frac{\alpha}{2}A-i \frac{\beta_2}{2} \frac{\partial^2 A}{\partial T^2}+i\gamma|A|^2A
$$

displays how the envelope and phase of an optical pulse change as it propagates through an optical fiber, taking into account attenuation $\alpha$ , group velocity dispersion (GVD) $\beta_2$ and self-phase modulation (SPM) $\gamma$ caused by nonlinearity.

This article will demonstrate the use of the Split-Step Fourier method to solve the Nonlinear Schrödinger Equation in Python.

This article is also available in 简体中文, Français.

the Basic Idea of Split-Step Fourier method

Optical pulses are generally represented by the envelope $A$ and the carrier wave $E$ .

Because the effect of self-phase modulation $\gamma$ on the pulse only has an analytical solution in the time domain:

$$
A(t, z+\Delta z)=A(t, z)e^{i\gamma \Delta z|A(t, z)|^2}
$$

The effect of group velocity dispersion $\beta_2$ on the pulse only has an analytical solution in the frequency domain:

$$
\tilde{A}(\omega, z+\Delta z)=\tilde{A}(\omega, z)e^{i\frac{\beta_2}{2}(\omega-\omega_0)^2\Delta z}
$$

Therefore, it is necessary to first calculate the effect of SPM in the time domain, then Fourier transform to the frequency domain to calculate the effect of GVD and attenuation, and finally use the inverse Fourier transform to return to the time domain.

The basic idea can be expressed as:

$$
A(t, z+\Delta z)= \underbrace{iFFT}_4 [\underbrace{e^{i\frac{\beta_2}{2}(\omega-\omega_0)^2\Delta z-\frac{\alpha}{2}\Delta z}}_3 \underbrace{FFT}_2[\underbrace{e^{i\gamma|A(T, z)|^2\Delta z} A(T, z)}_1]]
$$

Results Display (multiple figures warning)

The source code could be found in my GitHub repository. Click the moon icon in the upper right corner to turn on dark mode for a better experience.

The effects of attenuation, dispersion, and self-phase modulation on the pulse are displayed separately, followed by the results of their combined action.

Effects of attenuation only

The attenuation of typical optical fibers is 0.2 dB/km@1550nm. The following results show the power change of the output pulse in the time domain when the input Gaussian pulse enters a 1km fiber with only attenuation effects.

The following results show the power change of the output pulse in the frequency domain when the input Gaussian pulse enters a 1km fiber with only attenuation effects.

From the changes in the input and output pulses, it can be seen that only part of the energy is attenuated in the 1km fiber.

Effects of dispersion only

The group velocity dispersion parameter $\beta_2$ is set to $+100*10^3fs^2/m$. The following results show the power change of the output pulse in the time domain when the input Gaussian pulse enters a 1km fiber with only dispersion effects.

The following results show the change in the pulse intensity in the time domain as the transmission distance increases after inputting a Gaussian pulse into a 1km optical fiber with only chromatic dispersion effect.

The following results show the chirp change of the output pulse in the time domain when the input Gaussian pulse enters a 1km fiber with only dispersion effects.

Dispersion causes the pulse to broaden in the time domain, with low-frequency light accumulating at the leading edge of the pulse and high-frequency light accumulating at the trailing edge (the negative time axis corresponds to the leading edge of the pulse, and the positive axis corresponds to the trailing edge of the pulse). This corresponds to negative (red) chirp ( $\beta_2>0$ ) (normal dispersion).

Effects of self-phase modulation only

非线性系数 $\gamma$ 设置为 $10*10^{-3}rad/(W\cdot m)$ 。以下结果显示了输入高斯脉冲进入只有自相位调制效应的1km光纤后在频域上输出脉冲的变化。

以下结果显示了输入高斯脉冲进入只有自相位调制效应的1km光纤后随着传输距离的增加在频域上脉冲的频率变化。

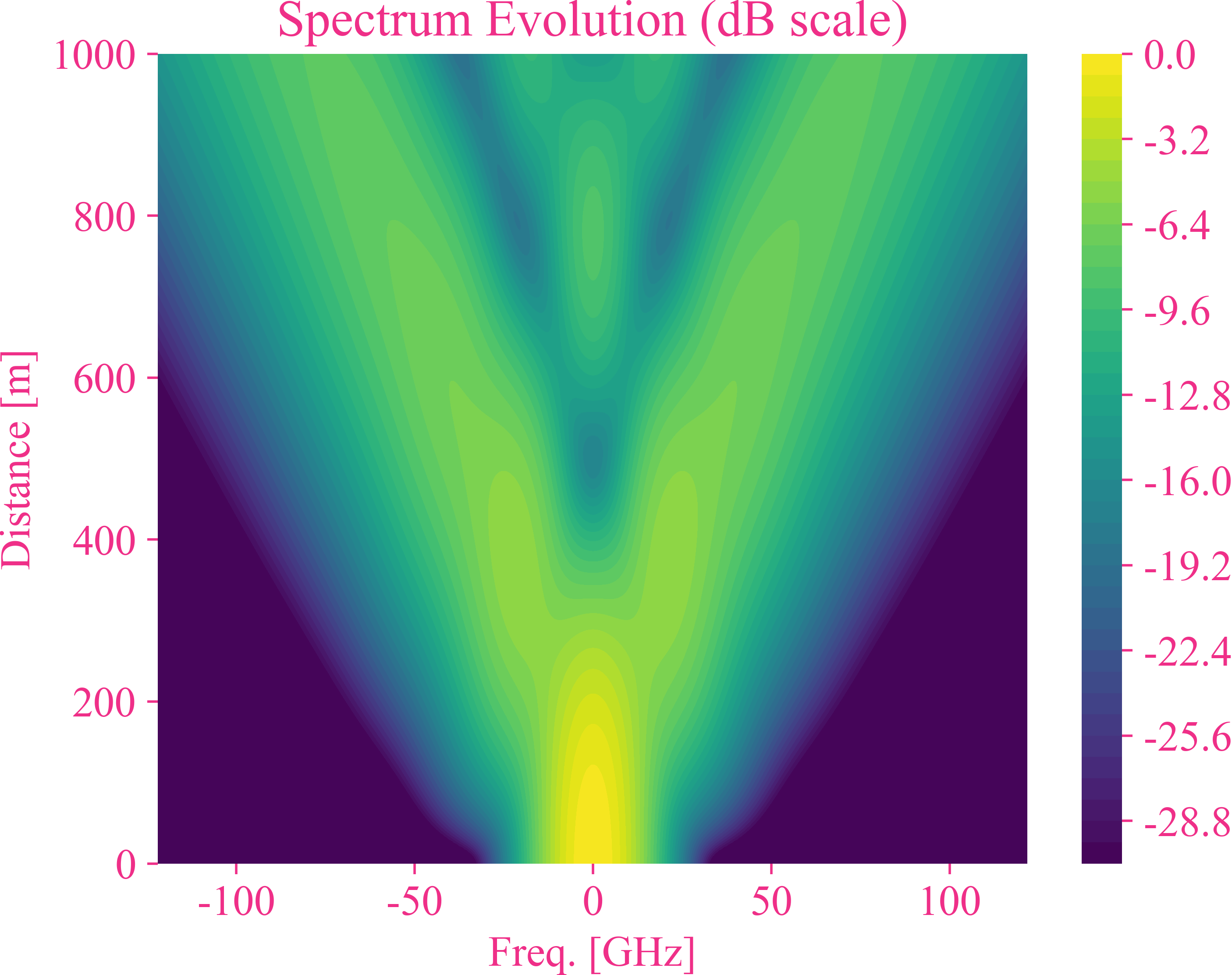
以下结果显示了输入高斯脉冲进入只有自相位调制效应的1km光纤后随着传输距离的增加在频域上脉冲的频率变化的3D视图。

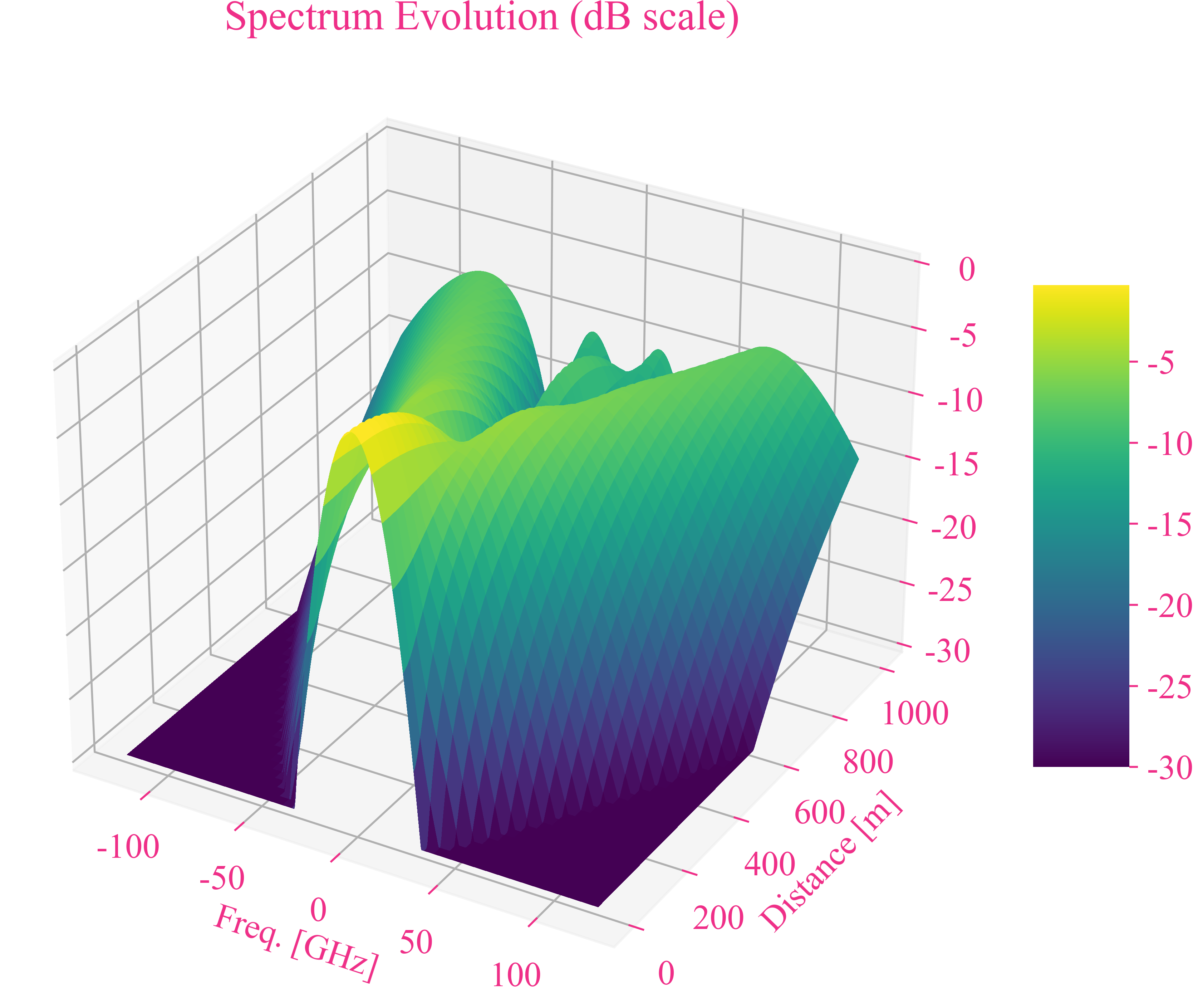
从以上结果可以看出，自相位调制改变了脉冲的频谱。中心频率功率减小并向两边进行展宽，分别分开成两个对称的峰，随着传输距离的增加，两个峰之间又出现两个对称的小峰值。

综合考虑衰减、色散和自相位调制

光纤的参数设置为：

• 光线长度为 $1000m$
• 衰减为 $0.2 dB/km@1550nm$
• 群速度色散参量 $\beta_2$ 为 $+100*10^3fs^2/m$
• 非线性系数 $\gamma$ 设置为 $10*10^{-3}rad/(W\cdot m)$

仿真参数设置为：

• 时域
  • 脉冲宽度[-60, 60]ps
  • 强度截止范围-30dB
• 频域
  • 频谱范围~[-120, 120]GHz
  • 强度截止范围-30dB

时域的结果

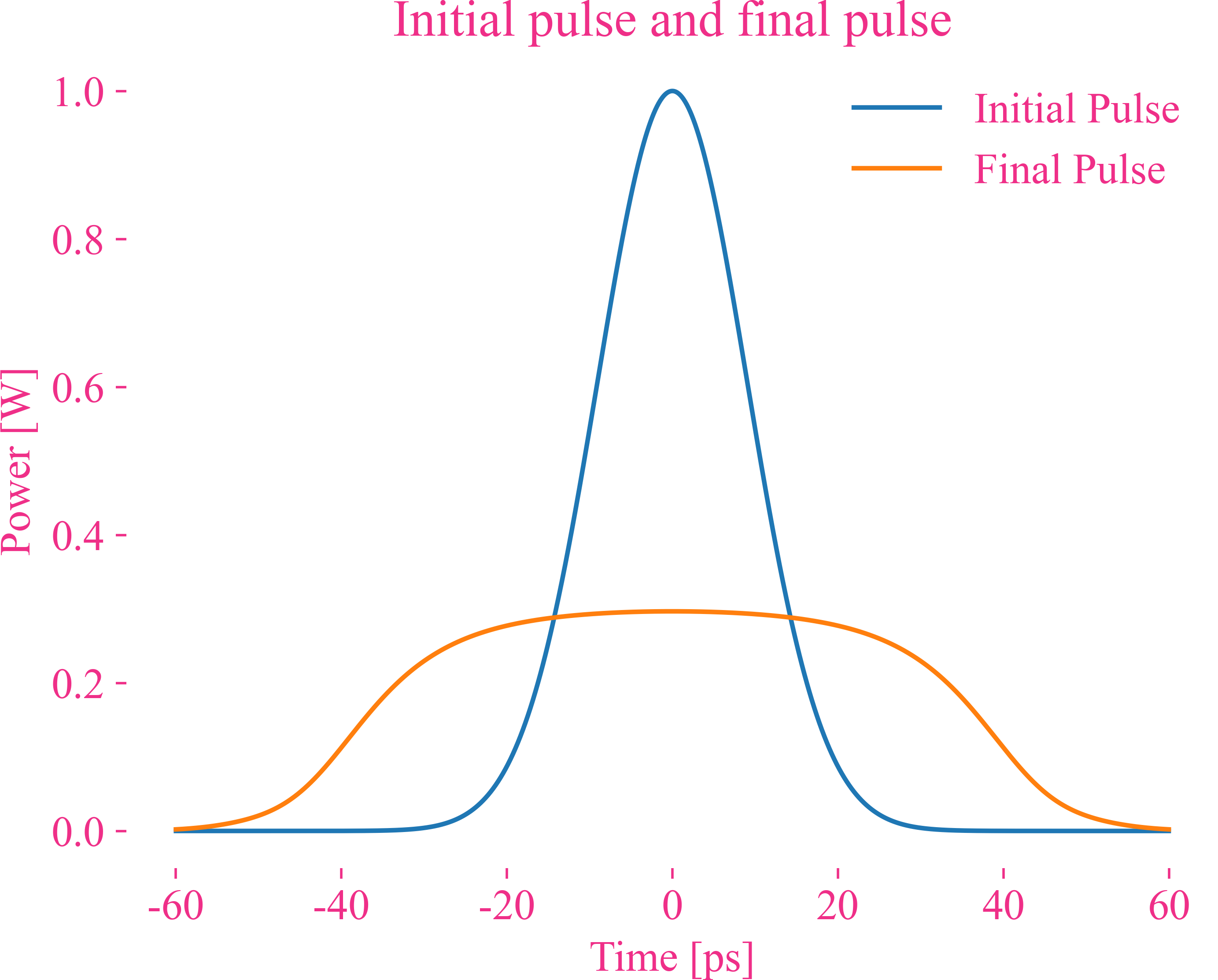
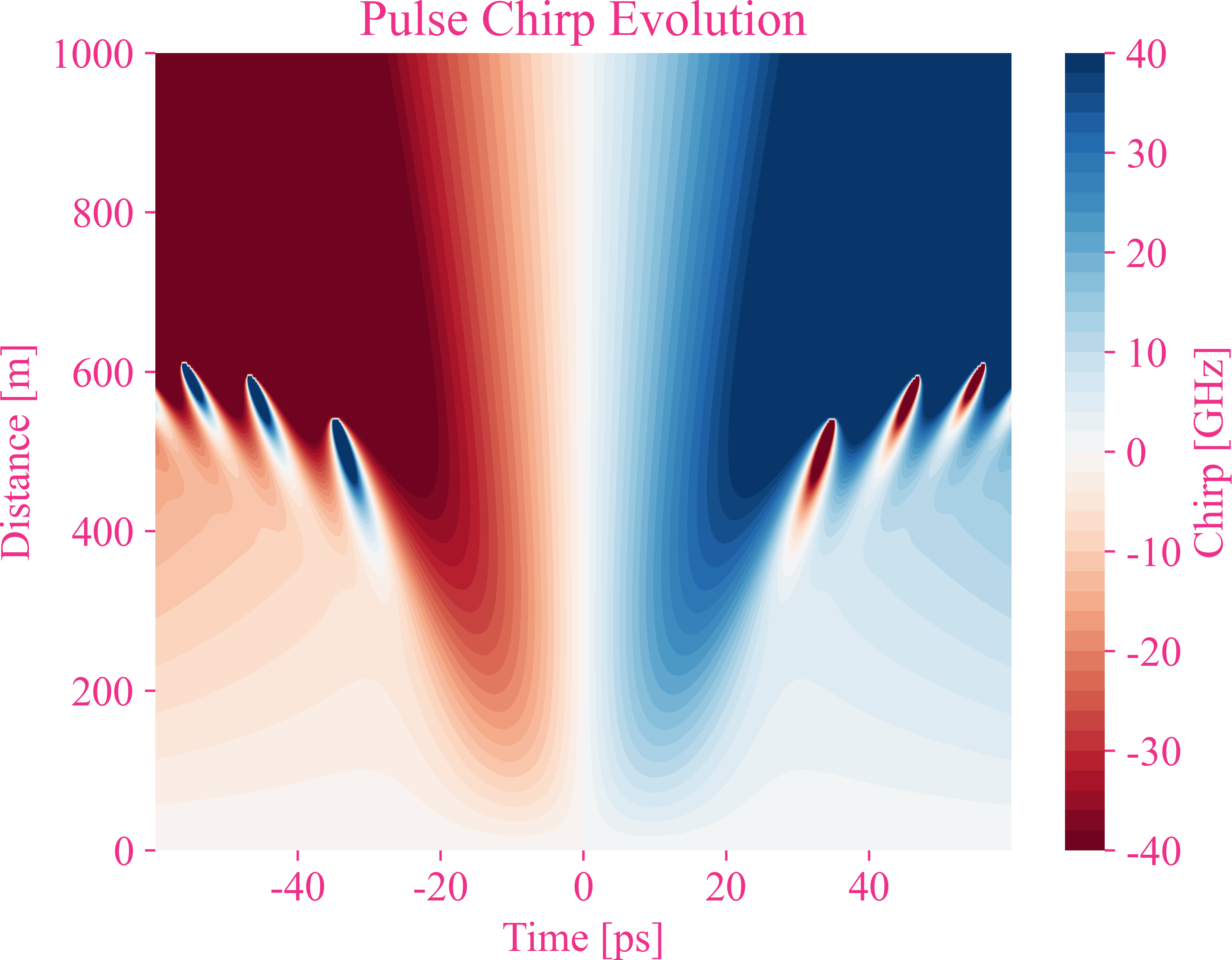
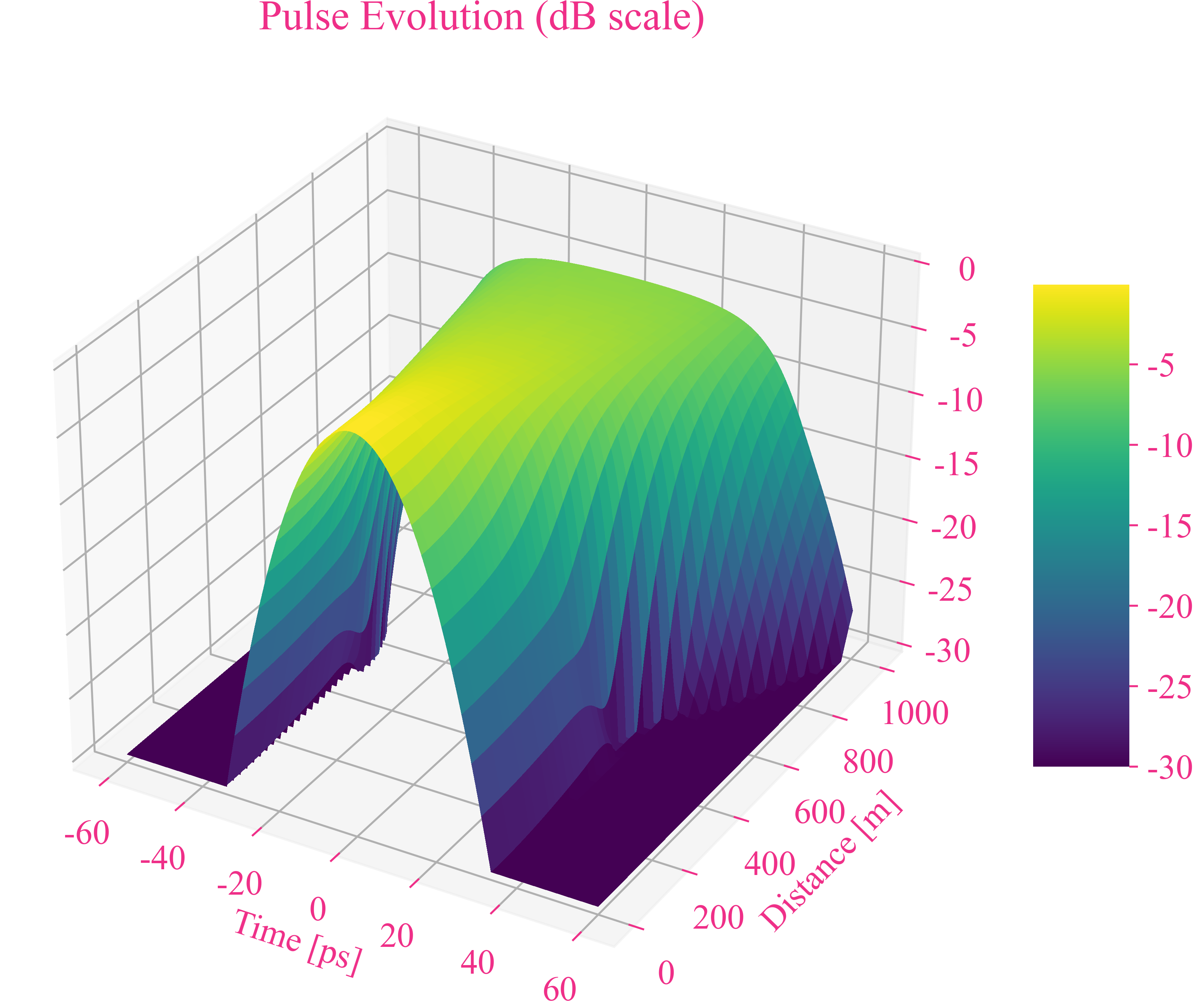
频域的结果

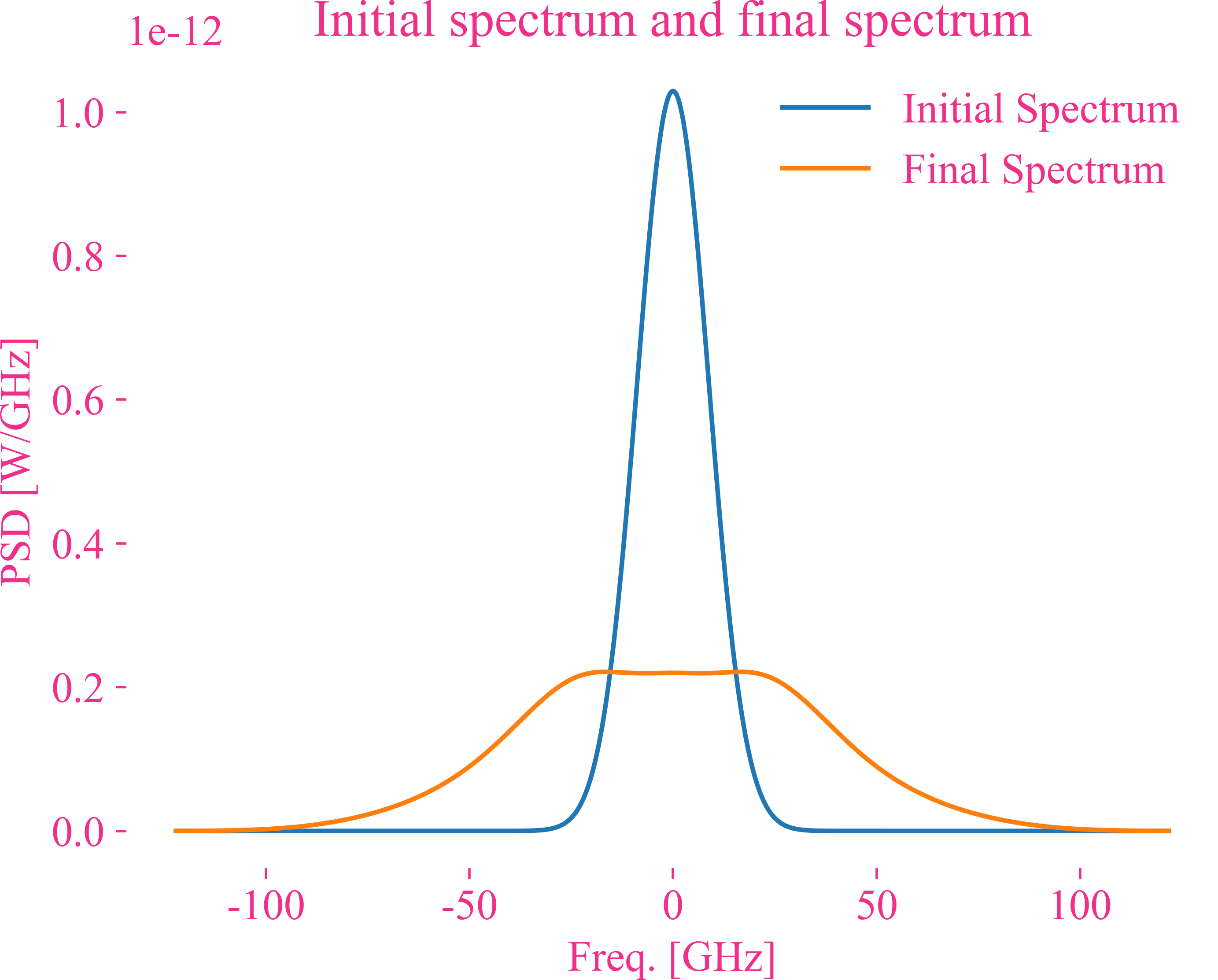
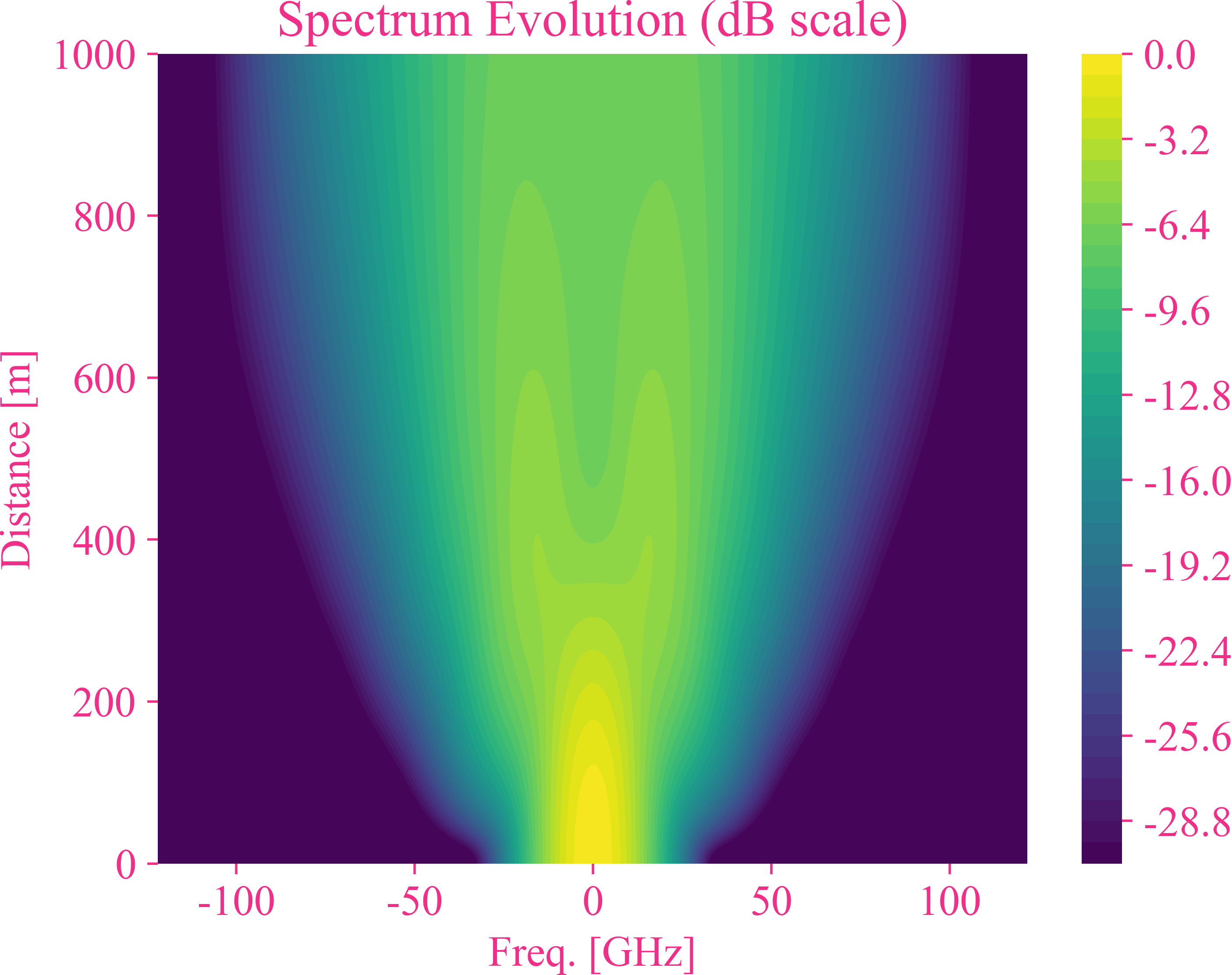
附录

附上部分生成综合考虑衰减、色散和自相位调制图片的源代码作为参考。

plot.pySSFM.ipynb

import numpy as np
from scipy.fftpack import fft, ifft, fftshift, ifftshift, fftfreq
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import cm

global pi; pi=np.pi 

def plotFirstAndLastPulse(matrix,fiber:Fiber_config,sim:SIM_config, nrange:int,**kwargs):
  t=sim.t[int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]*1e12
  plt.figure()
  plt.title("Initial pulse and final pulse")
  plt.plot(t,getPower(matrix[0,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]),label="Initial Pulse")
  plt.plot(t,getPower(matrix[-1,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]),label="Final Pulse")
  #plt.axis([-duration*5*1e12,duration*5*1e12,0,1.05*amplitude**2])
  plt.xlabel("Time [ps]")
  plt.ylabel("Power [W]")
  plt.legend()
  saveplot('first_and_last_pulse',**kwargs)
  plt.show()  
def plotPulseMatrix2D(matrix,fiber:Fiber_config,sim:SIM_config, nrange:int, dB_cutoff,**kwargs):
  #Plot pulse evolution throughout fiber in normalized log scale
  fig, ax = plt.subplots()
  ax.set_title('Pulse Evolution (dB scale)')
  t = sim.t[int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]*1e12
  z = fiber.zlocs 
  T, Z = np.meshgrid(t, z)
  P=getPower(matrix[:,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]  )/np.max(getPower(matrix[:,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]))
  P[P<1e-100]=1e-100
  P = 10*np.log10(P)
  P[P<dB_cutoff]=dB_cutoff
  surf=ax.contourf(T, Z, P,levels=40)
  ax.set_xlabel('Time [ps]')
  ax.set_ylabel('Distance [m]')
  cbar=fig.colorbar(surf, ax=ax)
  saveplot('pulse_evo_2D',**kwargs) 
  plt.show()

def plotPulseMatrix3D(matrix,fiber:Fiber_config,sim:SIM_config, nrange:int, dB_cutoff,**kwargs):
  #Plot pulse evolution in 3D
  fig, ax = plt.subplots(1,1, figsize=(10,7),subplot_kw={"projection": "3d"})
  plt.title("Pulse Evolution (dB scale)")

  t = sim.t[int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]*1e12
  z = fiber.zlocs 
  T_surf, Z_surf = np.meshgrid(t, z)
  P_surf=getPower(matrix[:,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]  )/np.max(getPower(matrix[:,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]))
  P_surf[P_surf<1e-100]=1e-100
  P_surf = 10*np.log10(P_surf)
  P_surf[P_surf<dB_cutoff]=dB_cutoff

  # Plot the surface.

  surf = ax.plot_surface(T_surf, Z_surf, P_surf, cmap=cm.viridis,
                        linewidth=0, antialiased=False)
  ax.set_xlabel('Time [ps]')
  ax.set_ylabel('Distance [m]')

  # Add a color bar which maps values to colors.

  fig.colorbar(surf, shrink=0.5, aspect=5)
  saveplot('pulse_evo_3D',**kwargs)
  plt.show()


def plotPulseChirp2D(matrix,fiber:Fiber_config,sim:SIM_config, nrange:int,**kwargs):
  #Plot pulse evolution throughout fiber in normalized log scale
  fig, ax = plt.subplots()
  ax.set_title('Pulse Chirp Evolution')
  t = sim.t[int(sim_config.number_of_points/2-nrange):int(sim_config.number_of_points/2+nrange)]*1e12
  z = fiber.zlocs 
  T, Z = np.meshgrid(t, z)

  Cmatrix=np.ones( (len(z),len(t))  )*1.0

  for i in range(fiber.ntraces):
    Cmatrix[i,:]=getChirp(t/1e12,matrix[i,int(sim_config.number_of_points/2-nrange):int(sim_config.number_of_points/2+nrange)])/1e9


  for kw, value in kwargs.items():
    if kw.lower()=='chirpplotrange' and type(value)==tuple:
      Cmatrix[Cmatrix<value[0]]=value[0]
      Cmatrix[Cmatrix>value[1]]=value[1]


  surf=ax.contourf(T, Z, Cmatrix,levels=40,cmap='RdBu')

  ax.set_xlabel('Time [ps]')
  ax.set_ylabel('Distance [m]')
  cbar=fig.colorbar(surf, ax=ax)
  cbar.set_label('Chirp [GHz]')
  saveplot('chirp_evo_2D',**kwargs) 
  plt.show()


def plotEverythingAboutPulses(pulseMatrix,fiber:Fiber_config,
                              sim:SIM_config, 
                              nrange:int, 
                              dB_cutoff,
                              **kwargs):

  print('  ')
  plotFirstAndLastPulse(pulseMatrix,fiber,sim, nrange,**kwargs)
  plotPulseMatrix2D(pulseMatrix,fiber,sim,nrange,dB_cutoff,**kwargs)
  plotPulseChirp2D(pulseMatrix,fiber,sim,nrange,**kwargs) 
  plotPulseMatrix3D(pulseMatrix,fiber,sim,nrange,dB_cutoff,**kwargs)

  print('  ')  


def plotFirstAndLastSpectrum(matrix,fiber:Fiber_config,sim:SIM_config, nrange:int,**kwargs):
  f=sim.f[int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]/1e9
  plt.figure()
  plt.title("Initial spectrum and final spectrum")
  plt.plot(f,getPower(matrix[0,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)])*1e9,label="Initial Spectrum")
  plt.plot(f,getPower(matrix[-1,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)])*1e9,label="Final Spectrum")
  plt.xlabel("Freq. [GHz]")
  plt.ylabel("PSD [W/GHz]")
  plt.legend()
  saveplot('first_and_last_spectrum',**kwargs)
  plt.show()

def plotSpectrumMatrix2D(matrix,fiber:Fiber_config,sim:SIM_config, nrange:int, dB_cutoff,**kwargs):
  #Plot pulse evolution throughout fiber in normalized log scale
  fig, ax = plt.subplots()
  ax.set_title('Spectrum Evolution (dB scale)')
  f = sim.f[int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]/1e9 
  z = fiber.zlocs 
  F, Z = np.meshgrid(f, z)
  Pf=getPower(matrix[:,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]  )/np.max(getPower(matrix[:,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]))
  Pf[Pf<1e-100]=1e-100
  Pf = 10*np.log10(Pf)
  Pf[Pf<dB_cutoff]=dB_cutoff
  surf=ax.contourf(F, Z, Pf,levels=40)
  ax.set_xlabel('Freq. [GHz]')
  ax.set_ylabel('Distance [m]')
  cbar=fig.colorbar(surf, ax=ax) 
  saveplot('spectrum_evo_2D',**kwargs) 
  plt.show()

def plotSpectrumMatrix3D(matrix,fiber:Fiber_config,sim:SIM_config, nrange:int, dB_cutoff,**kwargs):
  #Plot pulse evolution in 3D
  fig, ax = plt.subplots(1,1, figsize=(10,7),subplot_kw={"projection": "3d"})
  plt.title("Spectrum Evolution (dB scale)")

  f = sim.f[int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]/1e9 
  z = fiber.zlocs 
  F_surf, Z_surf = np.meshgrid(f, z)
  P_surf=getPower(matrix[:,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]  )/np.max(getPower(matrix[:,int(sim.number_of_points/2-nrange):int(sim.number_of_points/2+nrange)]))
  P_surf[P_surf<1e-100]=1e-100
  P_surf = 10*np.log10(P_surf)
  P_surf[P_surf<dB_cutoff]=dB_cutoff

  # Plot the surface.

  surf = ax.plot_surface(F_surf, Z_surf, P_surf, cmap=cm.viridis,
                        linewidth=0, antialiased=False)
  ax.set_xlabel('Freq. [GHz]')
  ax.set_ylabel('Distance [m]')

  # Add a color bar which maps values to colors.

  fig.colorbar(surf, shrink=0.5, aspect=5)
  saveplot('spectrum_evo_3D',**kwargs) 
  plt.show()


def plotEverythingAboutSpectra(spectrumMatrix, # 光谱矩阵
                               fiber:Fiber_config, # 光纤属性
                               sim:SIM_config,  # 仿真参数
                               nrange:int, # 画图范围
                               dB_cutoff, # 画图范围
                               **kwargs):

  print('  ')  
  plotFirstAndLastSpectrum(spectrumMatrix,fiber,sim, nrange,**kwargs)
  plotSpectrumMatrix2D(spectrumMatrix,fiber,sim,nrange,dB_cutoff,**kwargs)
  plotSpectrumMatrix3D(spectrumMatrix,fiber,sim,nrange,dB_cutoff,**kwargs)

  print('  ')  
#Plot pulses
nrange=600 # 时域的范围 -60，60ps
cutoff=-30 # 时域强度截止值dB

plotEverythingAboutPulses(pulseMatrix,fiber,sim_config,nrange,cutoff,savename='gaussian',chirpPlotRange=(-40,40))

#Plot spectra
nrange=400 # 频域的范围
cutoff=-30 # 频域强度截止值dB
plotEverythingAboutSpectra(spectrumMatrix,fiber,sim_config,nrange,cutoff,savename='gaussian')