Optical Soliton
This article contains several large .GIF images(~ 30 MB × 4), which may slow down the webpage loading speed.
To be improved…
When the group velocity dispersion and the self-phase modulation effect cancel each other out, the pulse maintains its shape during propagation in the optical fiber, forming an optical soliton.
Comparison of Group Velocity Dispersion and Self-Phase Modulation
The definition is as follows:
$$
N^2\equiv \frac{L_D}{L_{NL}}=\frac{\gamma P_0 T_0^2}{|\beta_2|}
$$
Optical Soliton
Hyperbolic secant pulses for $\beta_2<0$ and $\gamma>0$ .
First order
Second order
Third order
Fourth order
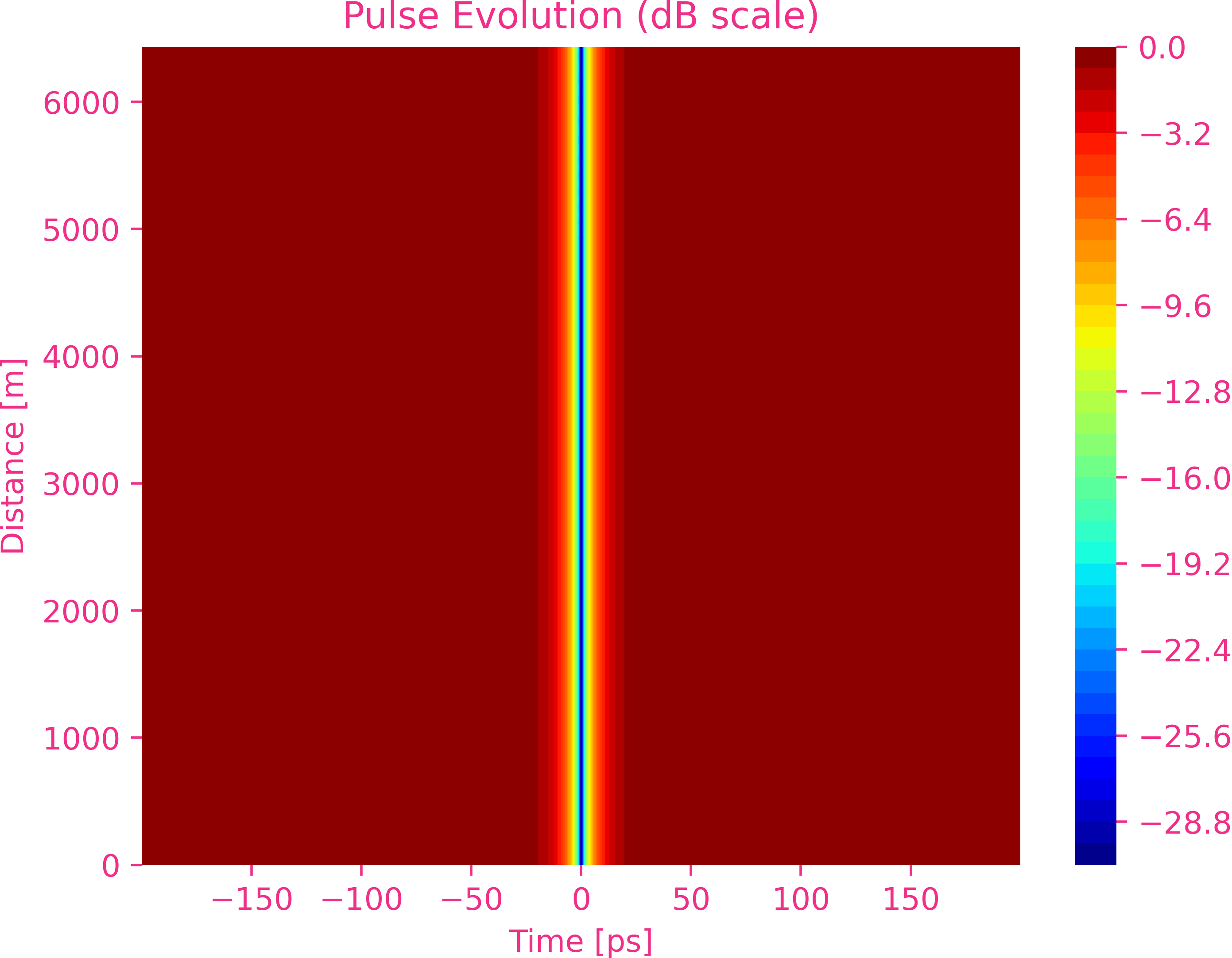
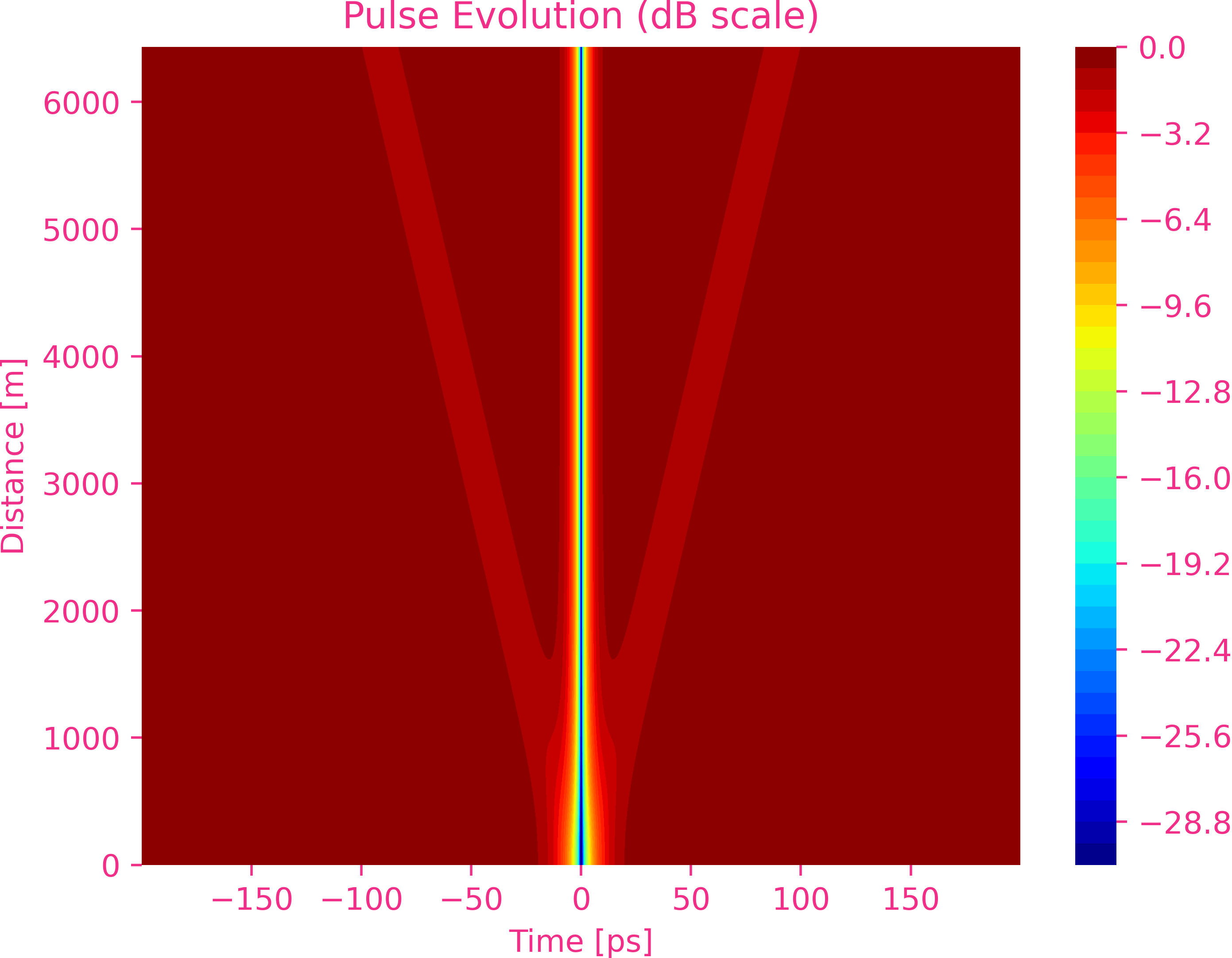
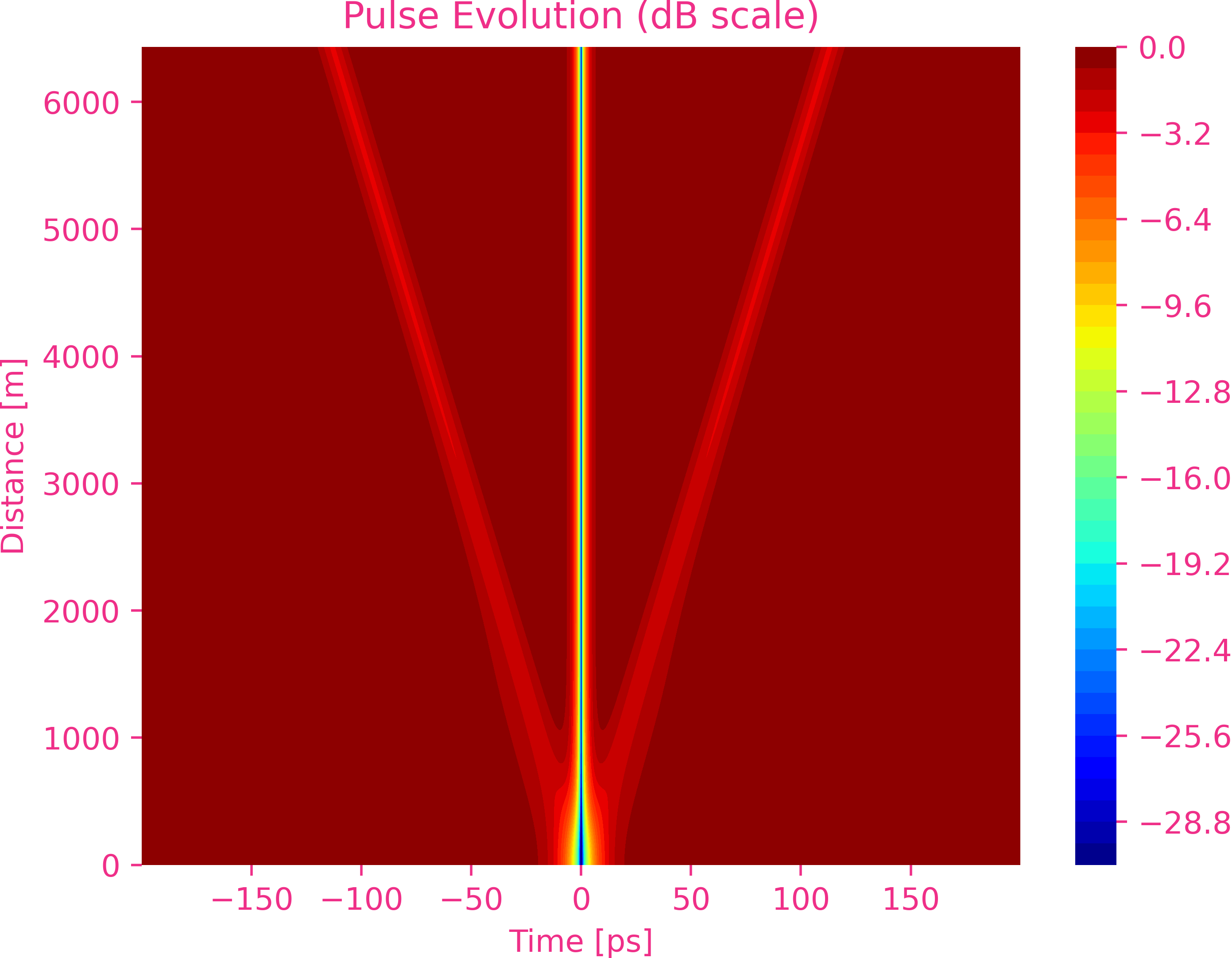
Dark Soliton
Hyperbolic tangent pulses for $\beta_2>0$ and $\gamma>0$ .
First order
Second order
Third order
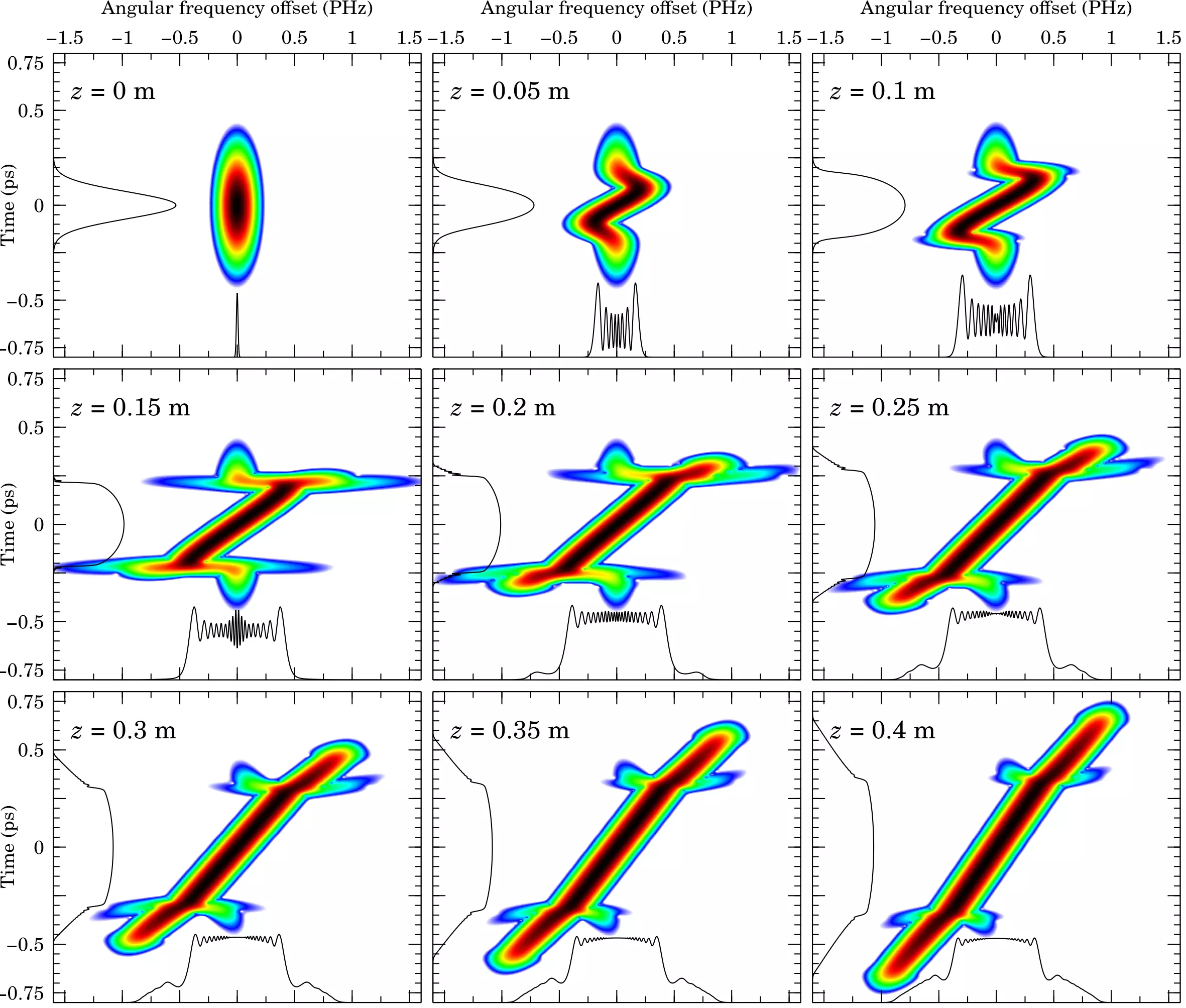
Optical Wave Breaking
Gaussian pulses experience optical wave breaking when $\beta_2>0$ and $\gamma>0$ .
© Marcus R.A. Newman, CC BY-NC-SA.
Optical Soliton